[ad_1]
September 28, 2023
When we need to decide the causal impact of a product or enterprise change at Spotify, A/B testing is the gold normal. However, in some circumstances, it’s not doable to run A/B assessments. For instance, when the intervention is an exogenous shock we will’t management, such because the COVID pandemic. Or when utilizing experimental management is infeasible, reminiscent of in the course of the annual supply of Spotify Wrapped. In these circumstances, we will show trigger and impact utilizing causal inference methods for observational information. One frequent approach we use for time sequence information is difference-in-differences (DID), which is straightforward to grasp and implement. However, drawing good conclusions from this technique with significance testing is extra advanced within the presence of autocorrelation, which is frequent in time sequence information. There are quite a few options for this difficulty, every with strengths and weaknesses.
We briefly describe the difference-in-differences technique and canopy three approaches to significance testing that appropriately deal with time sequence information — averaging, clustering, and permutation — together with some guidelines of thumb for when to make use of them. The outcomes of our simulation assessments present that permutation testing offers the very best stability between energy and false positives for datasets with small numbers of time sequence models and that the clustered normal error strategy is superior for bigger datasets. Averaging is broadly protecting of false positives however at an important price to statistical energy.
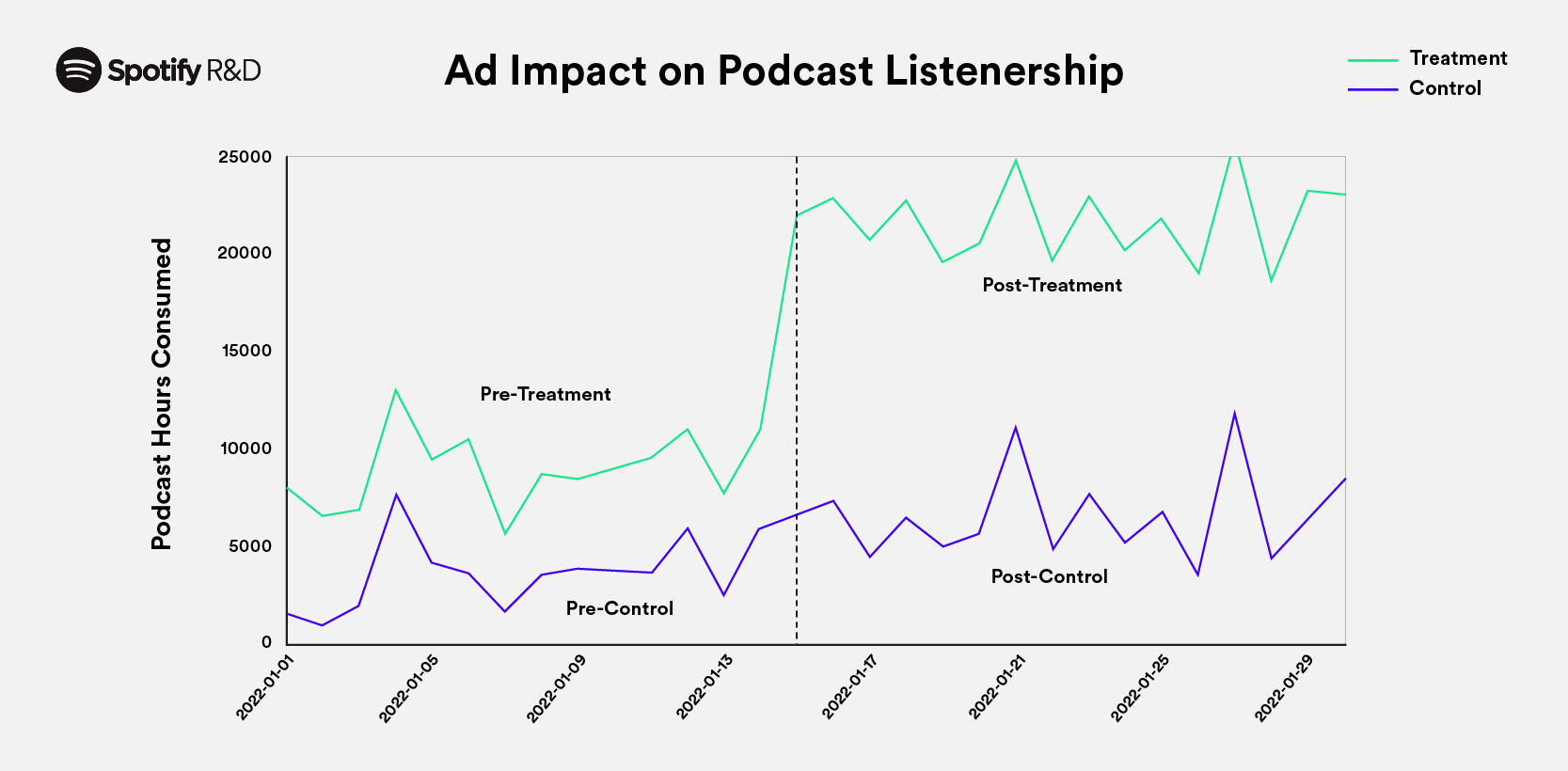
Suppose we need to improve podcast listening, so we spend advertising and marketing {dollars} selling a specific present. We’d like to determine the impression of the spend on present listening, however we will’t run an A/B check as a result of we don’t have a manner of controlling whether or not off-platform advertising and marketing reaches solely our remedy group and never our management group. We may look as an alternative on the distinction in listening after versus earlier than the advertising and marketing marketing campaign. However, present listening may improve or lower over time for plenty of causes unrelated to our advertising and marketing efforts (e.g., platform progress, consumer engagement seasonality, episode releases, and many others.), so a easy post-intervention/pre-intervention distinction could possibly be deceptive.
To appropriately perceive our advertising and marketing impact, we may make use of the favored causal inference approach for time sequence information referred to as difference-in-differences, or DID. Here we use DID to manage for components unrelated to advertising and marketing by using time sequence information for one more present, which was measured on the identical time factors however had no advertising and marketing marketing campaign. The concept is that this management time sequence ought to exhibit the identical tendencies in listening because the time sequence for the present we marketed — besides for the tendencies attributable to our advertising and marketing efforts. It estimates what would have occurred to our marketed present if we had not run the marketing campaign and lets us subtract all the opposite results from the handled present, leaving solely our advertising and marketing impact.
To do that, we take two variations. First, we subtract the listening information earlier than the advertising and marketing intervention from the info after the intervention. We do that for each remedy and management. The remedy distinction comprises our advertising and marketing impact and different results, which we’re not involved in. The management distinction comprises solely these results of no curiosity. Second, we subtract these two variations, eradicating the impression of the components we’re not involved in and isolating the causal impact of our advertising and marketing efforts (Figure 1).
Data above is for illustrative functions solely.
Estimating DID
DID is usually estimated with a linear mannequin of the shape:
Y = B0 + B1 * IsTreatment + B2 * IsPost + B3 * IsTreatment * IsPost + e
Where B0 is the coefficient for intercept, IsTreatment is an indicator (0 or 1) for the remedy time sequence, IsPost is an indicator for the pre- and post-intervention time factors, and the interplay IsTreatment * IsPost codes for the difference-in-differences we’re involved in, which is estimated by B3.
This sort of linear mannequin is handy to make use of, can readily deal with a number of remedy and/or management time sequence (or models), and might be expanded to incorporate nuisance covariates. When fitted through normal statistical software program, the output additionally options an ordinary error and p-value estimate to grasp the importance of the DID end result. However, typical options like extraordinary least squares (OLS) will usually get the importance check flawed and shouldn’t be trusted.
DID estimates are made utilizing time sequence information through which the observations usually are not impartial, however are usually correlated with each other. This autocorrelation distorts standard-error estimates when they’re computed within the ordinary manner and might result in inaccurate significance assessments and dangerous choices.
How does autocorrelation trigger this downside? Imagine producing a dataset the place every subsequent remark is created by taking the final remark and including some random noise to it. In this random stroll time sequence, the info are positively autocorrelated: the info factors close to each other in time are usually just like each other (this may be noticed quantitatively by correlating the sequence with a lagged copy of itself, and thru assessments such because the Durbin Watson). This is problematic as a result of every information level is partly defined by these previous it, so the quantity of data contained within the information is smaller than what a depend of the variety of observations would recommend. Statistical energy grows with pattern measurement, nevertheless it grows extra slowly for these positively autocorrelated information as a result of the observations aren’t speaking completely impartial data. As a end result, normal statistical software program routines are overconfident when estimating normal errors and declare significance too liberally.
Time sequence information may be negatively autocorrelated, the place information factors differ systematically from one time lag to a different. Negative autocorrelation has the alternative impact of constructive autocorrelation on normal errors. It creates underconfidence, with normal errors which might be too massive and significance assessments which might be too conservative. Autocorrelation of any type might be pernicious to good data-based decision-making. While we encounter each types within the information we work with, we observe constructive autocorrelation extra generally, so we concentrate on it within the simulations described under. The cures we discover, nevertheless, are broadly relevant, whatever the signal of the autocorrelation.
We examined this downside by creating synthetic time sequence with constructive autocorrelation, becoming DID fashions, and analyzing the importance check outcomes. Importantly, we added no causal impact to the “treatment” time sequence in these simulations (half of the simulated time sequence models have been labeled as remedy).
If the usual errors have been appropriately estimated on the significance stage we used (alpha=0.05), we’d count on to detect significance at a 5% price (false constructive price), regardless of no added remedy impact. However, as a result of autocorrelation in our information, the false constructive price was over 30% (Figure 2), over 5 occasions too excessive!
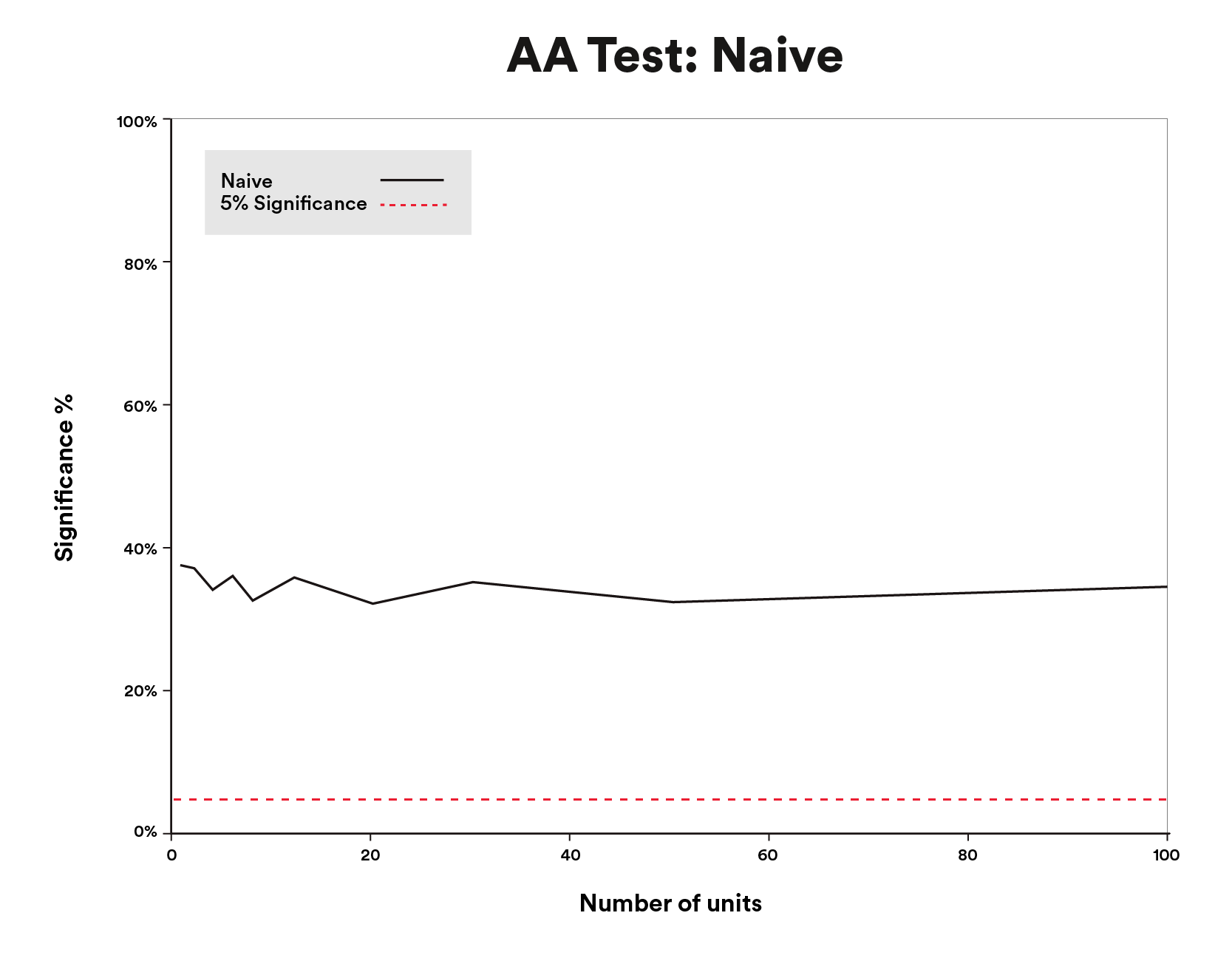
Data above is for illustrative functions solely.
How can we precisely estimate significance?
A false constructive price of over 30% is way too excessive to depend on this method to make good product and enterprise choices. Fortunately, quite a few strategies have been proposed to appropriately estimate significance with autocorrelated information. We examined three approaches that seem steadily within the literature — averaging, clustering, and permutation — and examined their relative professionals and cons.
Averaging
The easiest strategy we used to take away autocorrelation was averaging. With averaging, we escape the autocorrelation downside by taking the imply of every time sequence unit earlier than and after the intervention. For every unit in an evaluation, this produces a single pre- and post-intervention information level (Figure 3). Because the info at the moment are basically now not a time sequence, the autocorrelation downside is eradicated.
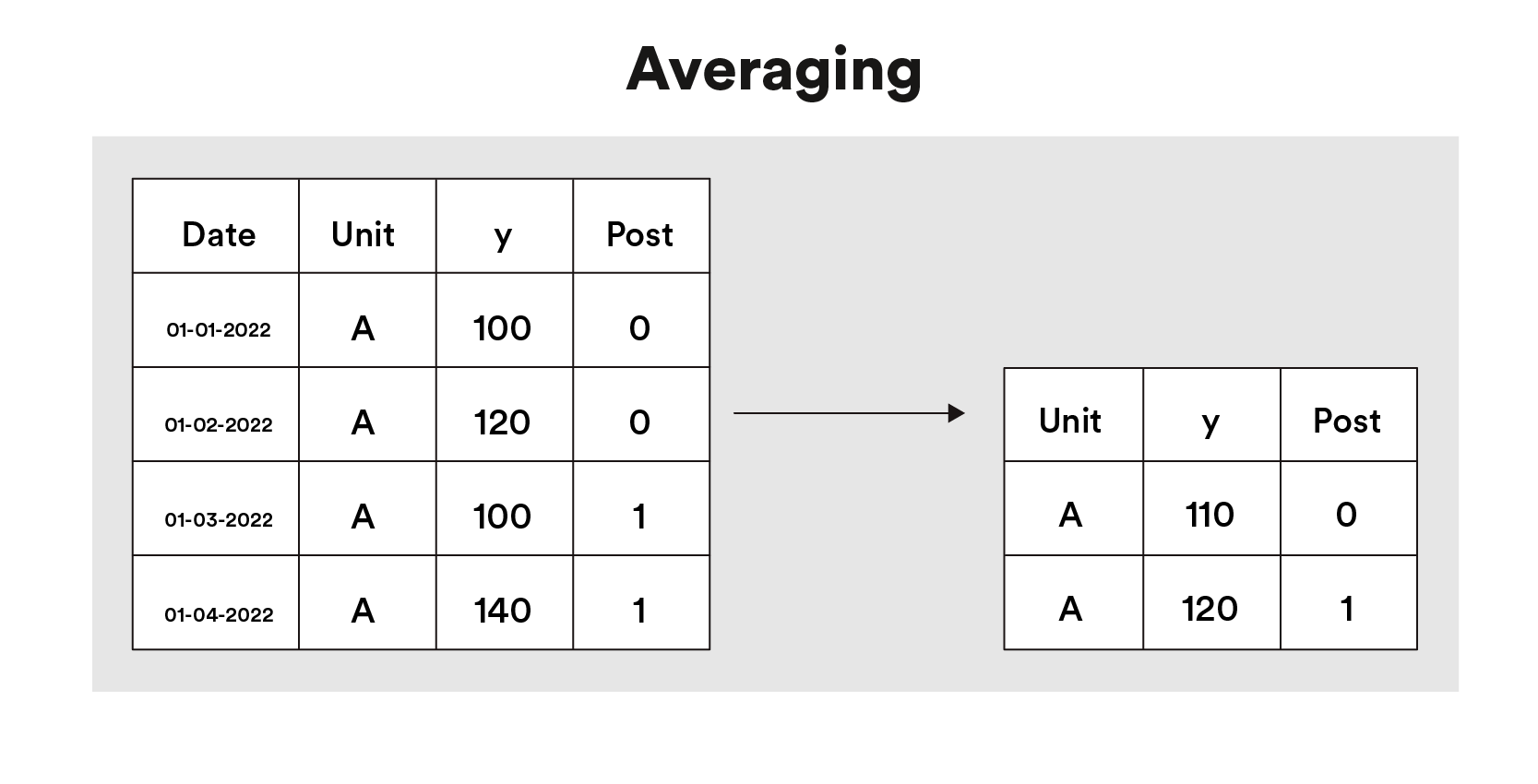
Data above is for illustrative functions solely.
Ordinary strategies for computing normal errors and significance testing can be utilized on averaged information with out difficulty. We examined this technique with our simulated information and located the false constructive price fell into the anticipated vary (5%, Figure 4). However, by averaging, we’re usually dramatically decreasing the dimensions of our information and subsequently, our energy to discover a important end result.
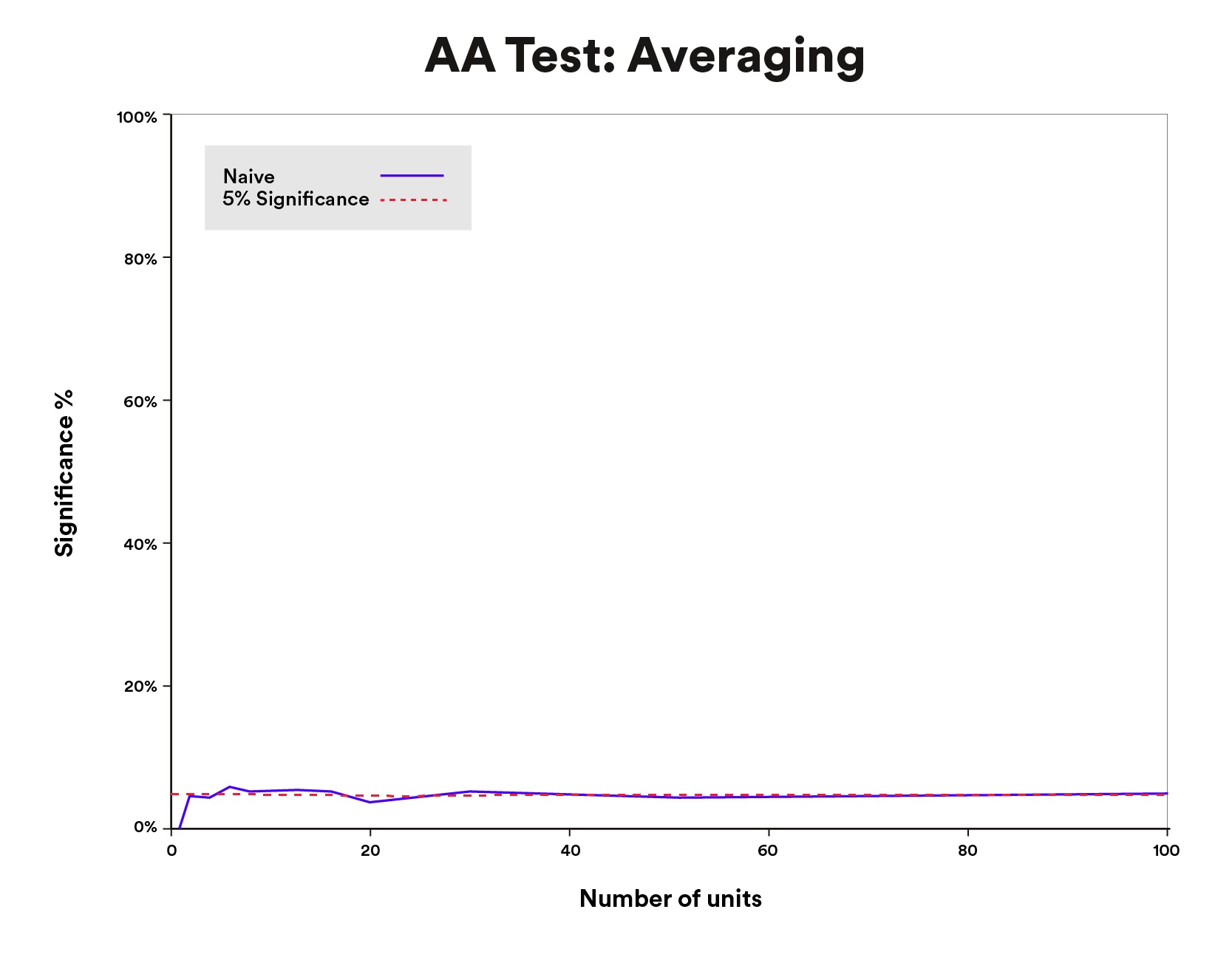
Data above is for illustrative functions solely.
Clustered normal errors
Unlike averaging, the clustered-standard-errors strategy makes use of the complete dataset. It’s additionally straightforward to estimate utilizing frequent statistical packages. You simply want to inform the software program what your clusters are.
But what’s a cluster? It’s actually simply one other title for the time sequence unit we mentioned above. When defining a cluster, we need to group correlated information into the identical cluster. So sometimes, in time sequence evaluation, every time sequence turns into its personal cluster.
For instance, my utilization of Spotify at the moment is correlated with my utilization tomorrow. But somewhat than treating every day as an impartial measurement, the measurements ought to be grouped right into a cluster as a result of they’re correlated. Similarly, your utilization information are correlated over time and ought to be grouped right into a cluster. Your information and my information usually are not probably correlated, so they need to be grouped into completely different clusters.
These clusters can be utilized to assist us appropriately estimate statistical significance. Typically, the main points on how this works are defined through the linear algebra used to compute the specialised variance-covariance matrices that remedy the issue of correlated information. Here, we simply give the instinct for a way clustered normal errors work, and refer the reader to Cameron and Miller (2015) for extra particulars.
When we mannequin our clustered information, we sometimes assume that they’re correlated inside clusters however not throughout them — although there are circumstances the place extra refined correlation constructions are relevant, e.g., Ferman (2002). Common statistical software program routines for linear fashions like OLS assume zero correlation in all places, which is what will get us into bother with significance testing. With the clustered strategy, we estimate the correlations throughout the clusters utilizing the mannequin residuals. These residual errors are then used to compute the usual error of our estimated impact, which we subsequently use for significance testing. Because the within-cluster correlation has been immediately integrated into the standard-error estimate, bigger constructive autocorrelation within the information will lead to bigger standard-error estimates (somewhat than the smaller ones we’d see from normal statistical software program mannequin output). This protects us from the rise in false positives we’d count on in our positively autocorrelated time sequence information (see Figure 2).
To show how elevated constructive autocorrelation pertains to bigger normal errors (and subsequently fewer false positives) utilizing the clustered strategy, we simulated time sequence information with completely different quantities of within-cluster autocorrelation. We then match DID fashions with clustered normal errors to those information and recorded the residuals and normal errors. Figure 5 reveals that the strategy works as marketed: as constructive autocorrelation will increase, so too does residual error and subsequently normal error (plotted as 95% confidence intervals for visualization functions).
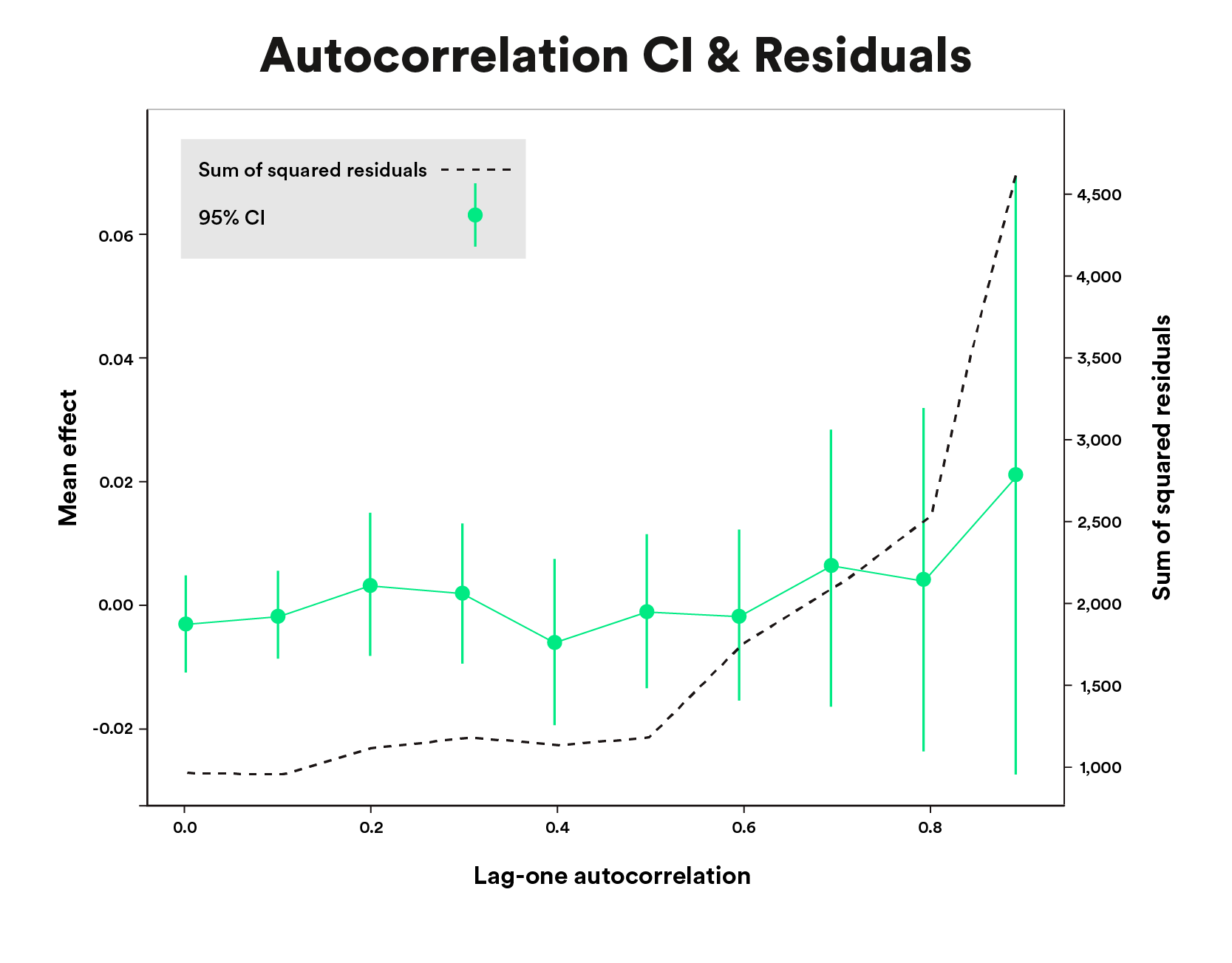
Data above is for illustrative functions solely.
It’s vital to notice that the speculation behind clustered normal errors says that this technique will converge to the true normal error because the variety of clusters goes to infinity. In follow, this implies if we now have too few clusters, the usual errors and thus mannequin inference will probably be incorrect. We explored this with simulated time sequence and located that the false constructive price was fairly excessive once we had few clusters (Figure 6), nevertheless it fell into the anticipated vary because the variety of clusters/models grew.
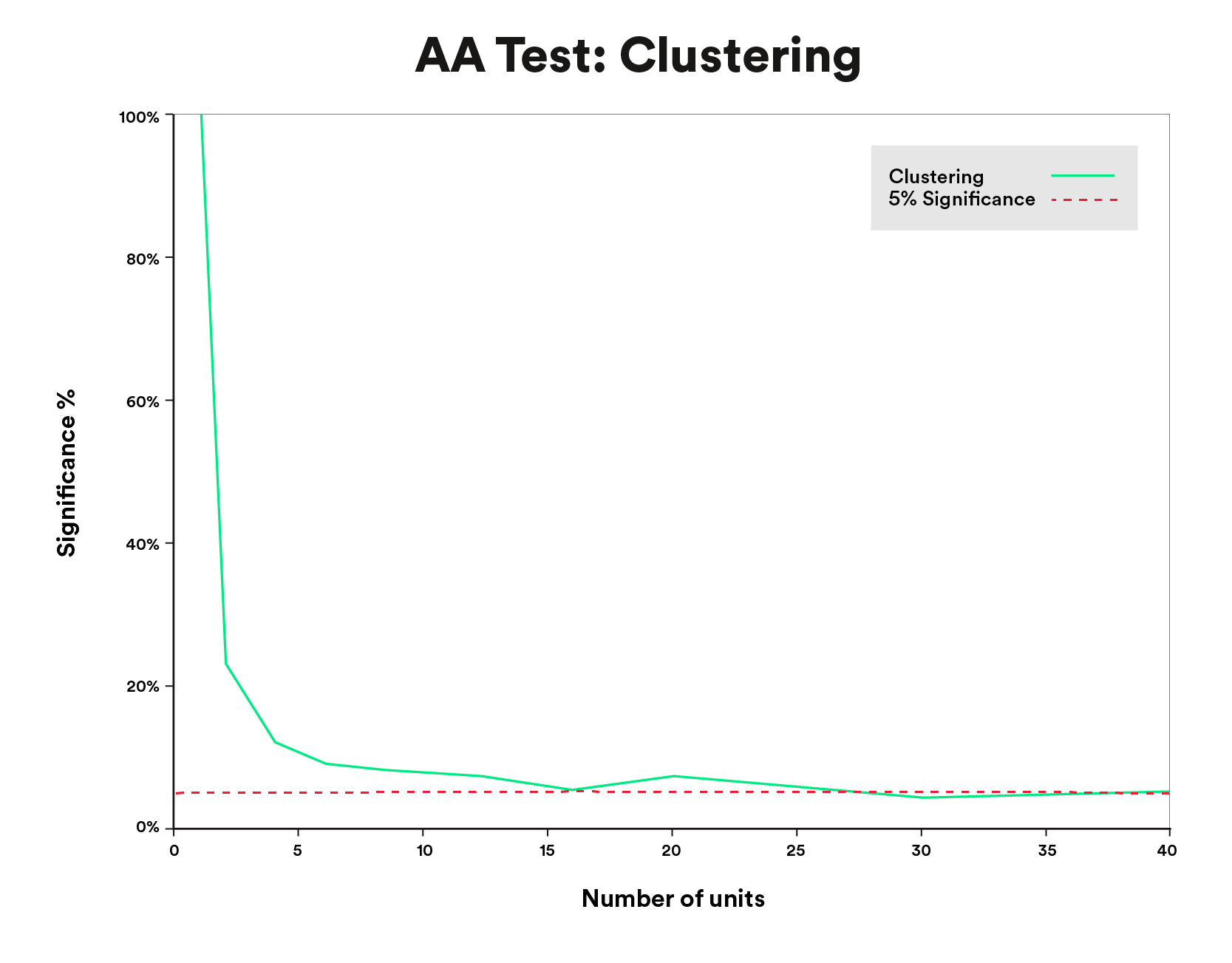
Data above is for illustrative functions solely.
Permutation testing
Permutation testing doesn’t take care of the autocorrelation difficulty immediately just like the clustering strategy however as an alternative renders it innocent by evaluating the relative rarity of the noticed outcomes to those who may have been noticed with the autocorrelated information.
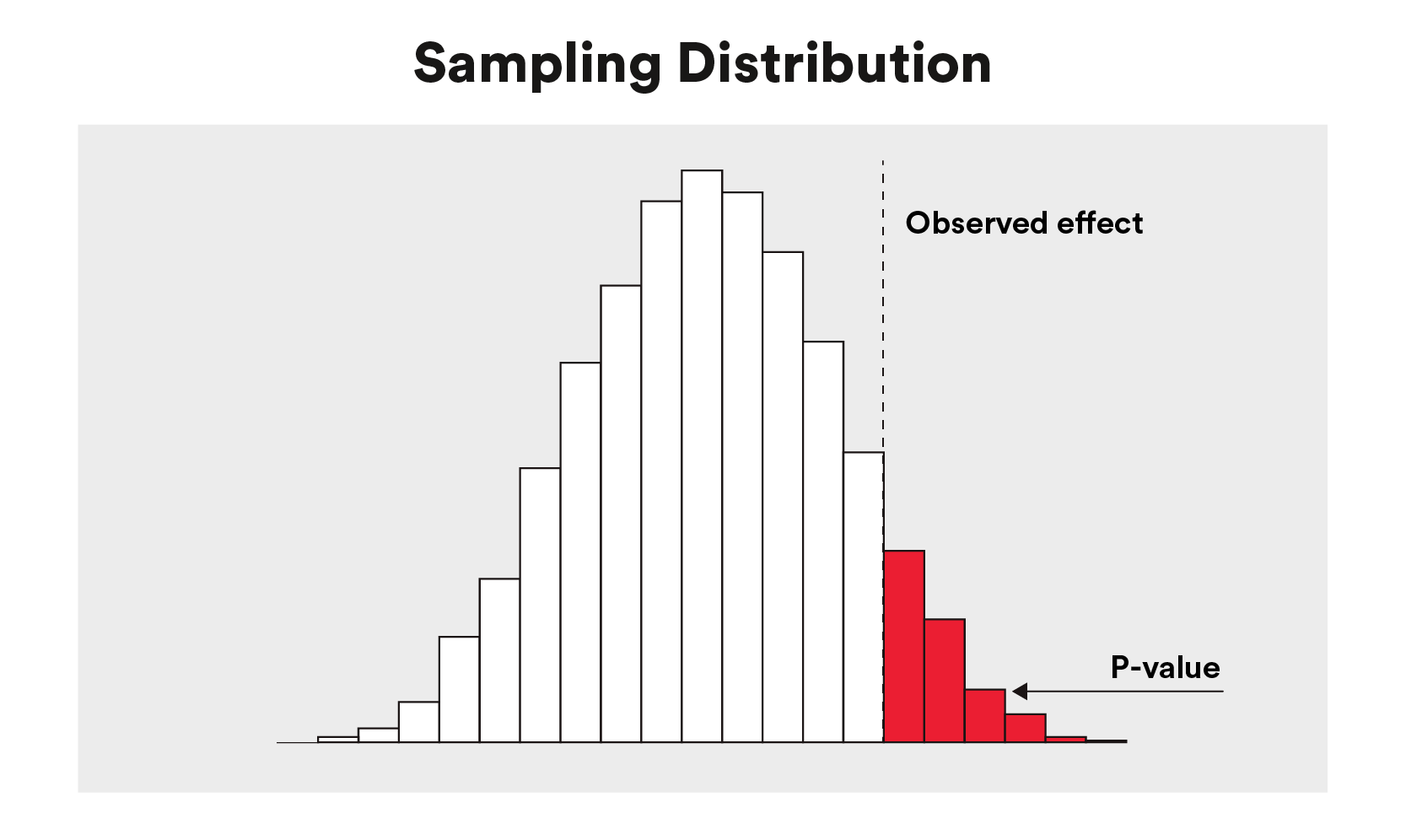
Let’s stroll via the permutation testing process. First, we mannequin our information to get the DID estimate. Next, we subtract the remedy impact from the handled time sequence for the time durations when the remedy was in impact. Then, we randomly shuffle the “treatment” and “control” labels for the time sequence models, permitting “treatment” to turn into “control” and vice versa, and use DID to estimate the causal impact of the “treatment”. We repeat this shuffling and estimating course of hundreds of occasions, recording the DID level estimate every time. This process offers us a sampling distribution of DID results we may have noticed if our intervention of curiosity had no impact on the handled time sequence models. This distribution can be utilized to grasp the importance of the noticed impact: its location within the distribution signifies the p-value (Figure 7).
We examined permutation testing with simulated time sequence with no causal impact. The false constructive price appropriately matched the alpha we set throughout a lot of the unit-size circumstances we thought of (Figure 8).
Values above are for illustrative functions solely.
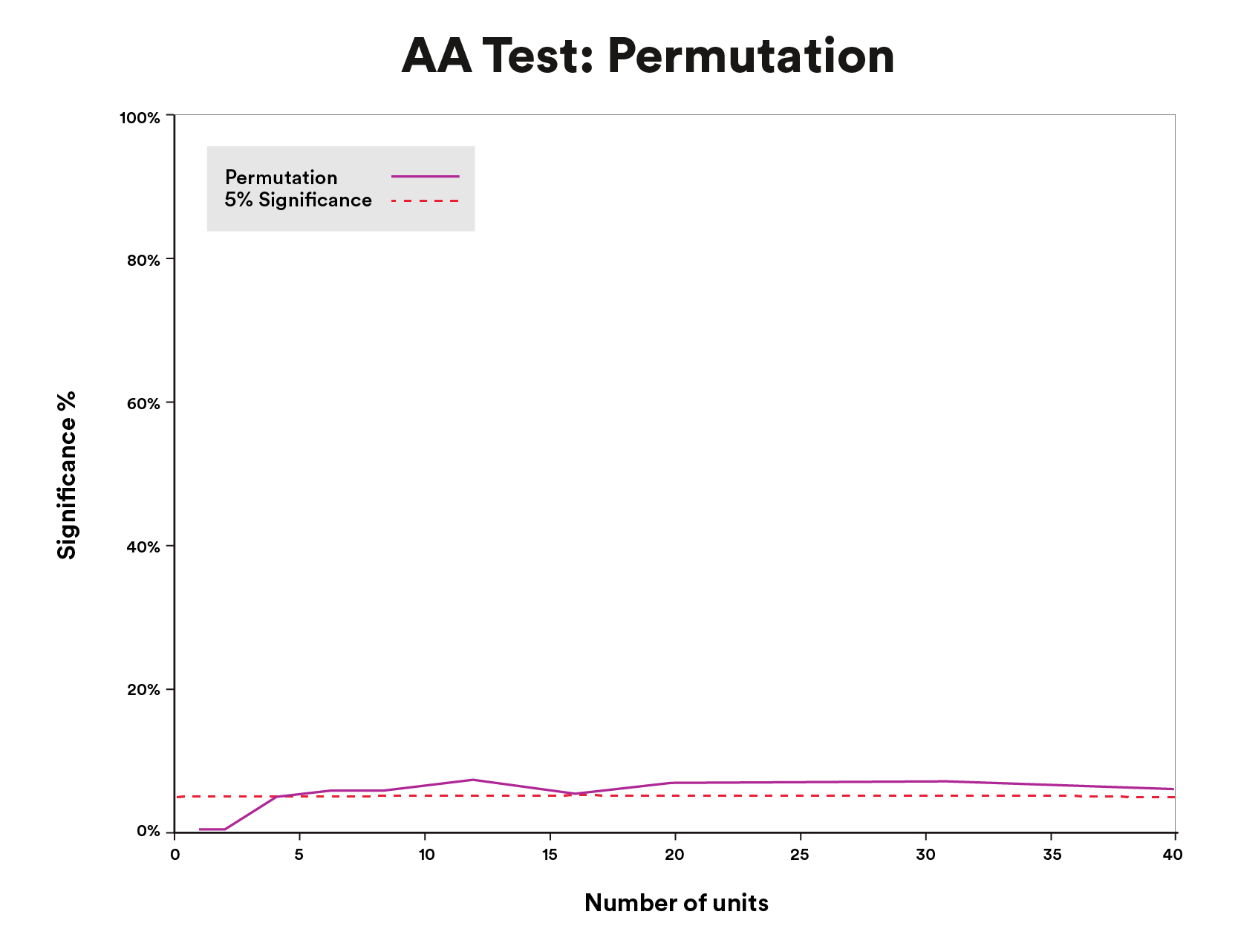
Data above is for illustrative functions solely.
Method comparability
In our simulations, all three approaches to the autocorrelation downside produced the anticipated false constructive price with sufficiently massive numbers of models (Figure 9). With few models, efficiency differed. (Note that whereas we point out particular unit sizes for our outcomes, efficiency will differ from one dataset to a different, so relative, somewhat than precise, sizes ought to be taken as steering.)
For very small numbers of models (one to 5 in our simulations) the clustering strategy confirmed excessive false constructive charges, and averaging and permutation testing confirmed anticipated or lower-than-expected false positives. While this initially seems to be a power of averaging and permutation, in actuality, all strategies finally break down when the variety of models will get small. For permutation testing, with only some models, there are only some permutations of the info, and subsequently a sampling distribution with only some values, which lacks the decision to usefully find the noticed end result on it to estimate a p-value. As a end result, these low-unit permutation assessments by no means declare significance, and subsequently can by no means emit false positives. Averaging fares barely higher, the place analytic statistics appropriately cowl very small numbers of models. However, when variance can now not be computed (e.g., evaluating a single information level to a different), false positives don’t exist as a result of significance assessments can’t be calculated.
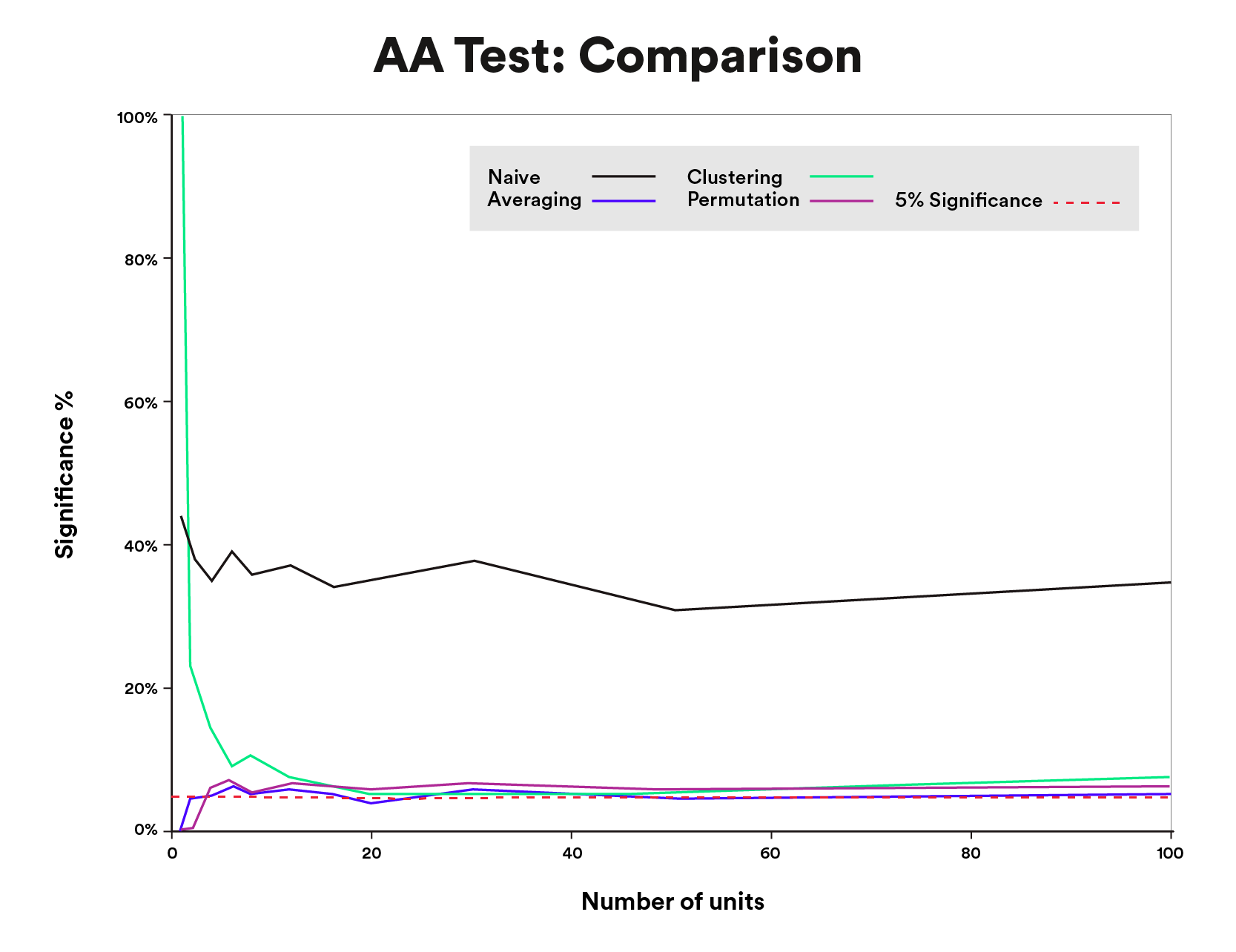
Data above is for illustrative functions solely.
For small, however not tiny, numbers of models (5 to 10 in our simulations), averaging and permutation testing outperformed clustering. Consistent with principle, we noticed that the clustering strategy continued to indicate elevated false constructive charges, whereas permutation and clustering confirmed charges matching expectation. Though clustering is appealingly easy to make use of in lots of statistical software program libraries, it might produce deceptive outcomes with small datasets.
Data above is for illustrative functions solely.
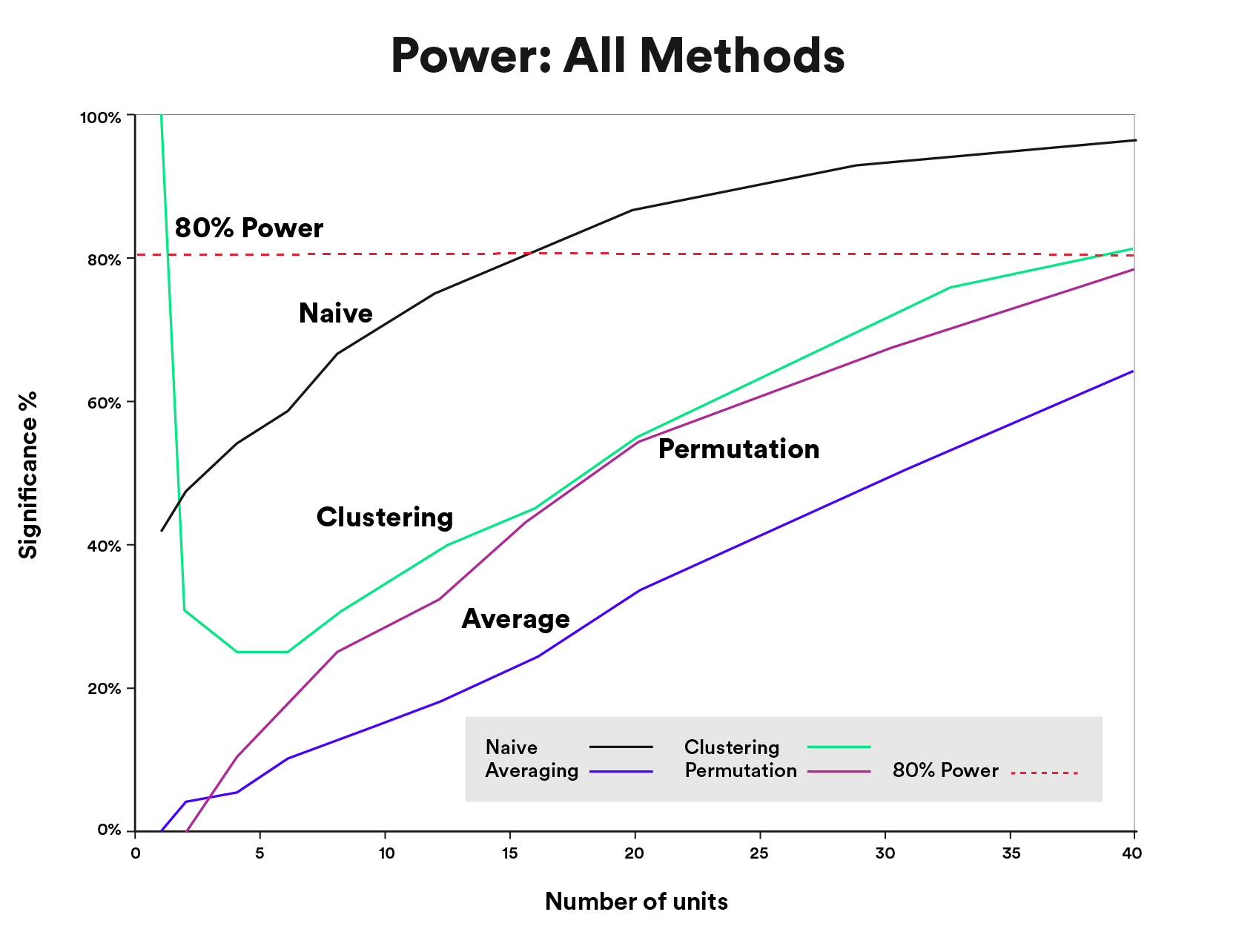
In addition to assessing false positives, we ran additional simulations to grasp the statistical energy provided by the completely different autocorrelation options (Figure 10). We simulated time sequence information the place we utilized a ten% relative informal impact to the handled time sequence within the post-treatment time durations and evaluated the variety of occasions we detected an impact (energy).
We discovered that each one strategies produced substantial decreases in energy in comparison with the naive technique, the place autocorrelation is ignored (and false positives are excessive), and relative to the frequent experimental design energy goal of 80% for the dimensions of the info we assessed. Averaging, which vastly lowered the dimensions of our information, unsurprisingly confirmed the most important discount in energy. Clustering and permutation testing confirmed related energy, besides with smaller numbers of models. Though clustering reveals an obvious energy benefit, in actual purposes the place the presence of an impact is unknown, this benefit comes at the price of a excessive false constructive price (see Figure 9). Clustering declares significance too liberally, catching true and false positives alike.
If you’ve got a lot of models, our outcomes recommend you need to use clustered normal errors. If the variety of models could be very massive so energy isn’t a problem, you may also think about averaging. At a big scale, we advise towards permutation testing owing to the computational burden it presents.
If you’ve got a small variety of models, our outcomes favor permutation testing to greatest retain energy whereas controlling for false positives. In this vary of knowledge, it might be value utilizing a number of approaches for a similar evaluation and contemplating how the ability and error trade-offs of every relate to the trade-offs of the choice at hand. As the variety of models will get very small, all of the strategies turn into unreliable. Averaging retains efficiency the longest, however at an important price in energy. With very small numbers of models, it’s value trying to find extra information.
At Spotify, we regularly encounter issues the place A/B assessments are unimaginable, however an understanding of trigger and impact has excessive enterprise worth. In these circumstances, causal inference methods reminiscent of DID might help us make good choices. However, DID fashions — and fashions of any autocorrelated time sequence information extra usually — require specialised strategies to keep away from errors in significance testing.
Here we used simulations to discover three approaches for addressing the issue of autocorrelation. We targeted on constructive autocorrelation, however the strategies investigated defend towards the issues attributable to damaging autocorrelation as properly. Unlike the naive (inaccurate) technique that’s normal output for linear fashions in most statistical software program, our simulations confirmed that use of those approaches produced false positives consistent with expectation. All strategies improved false constructive charges, however accuracy and statistical energy diversified throughout assessments as the dimensions of the info grew. For the vary of knowledge sizes we assessed, we discovered permutation and clustering to have the very best stability of false positives and energy for small and huge numbers of models, respectively. When conducting significance testing with time sequence information, it’s vital to contemplate how autocorrelation may produce deceptive outcomes and to decide on an applicable technique for the options of the issue at hand.
Acknowledgments
Thanks to Omar Farooque and Matt Hom for his or her enter and suggestions on earlier iterations.
Tags: experimentation
[ad_2]