[ad_1]
July 25, 2023
In Part 1 of this sequence, we launched the within-unit peeking downside that we name the “peeking problem 2.0”. We confirmed that shifting from single to a number of observations per unit in analyses of experiments introduces new challenges and pitfalls close to sequential testing. We mentioned the significance of being clear concerning the distinctions between measurement, metric, estimand, and estimator, and we exemplified these distinctions with so-called cohort-based metrics and open-ended metrics. In a small simulation, we confirmed that commonplace sequential exams mixed with open-ended metrics can result in inflated false constructive charges (FPRs).
In Part 2 of the sequence, we share some learnings from implementing sequential exams primarily based on knowledge with a number of observations per unit, i.e., so-called longitudinal knowledge.
We cowl the next subjects:
- Why we have to pay further consideration to longitudinal knowledge in sequential testing
- Practical issues for operating sequential exams with longitudinal knowledge
- How group sequential exams (GSTs) apply to longitudinal knowledge fashions, and a few GST-specific facets to be aware of
- Some concluding remarks on how Spotify applies sequential exams on longitudinal knowledge experiments
It’s not unusual to make use of longitudinal knowledge in on-line experimentation, and sometimes this requires no particular consideration when utilizing fixed-horizon evaluation. However, when combining longitudinal knowledge and sequential testing, longitudinal knowledge rapidly introduces specific challenges. To derive fixed-horizon exams for any check statistic, it’s enough to know its marginal sampling distribution. For sequential exams, we have to know the dependence construction of the vector of check statistics over the intermittent analyses. With one statement per unit, the dependence between check statistics solely comes from the overlapping pattern of unbiased items. With longitudinal knowledge, the covariance between the check statistics at two intermittent analyses comes each from new measurements of the identical items and the overlapping pattern between the analyses.
This would possibly look like a delicate distinction, however for sequential testing this complicates issues. We sometimes function below an assumption of unbiased measurements between items — however not inside items. The dependency inside items complicates the covariance construction of the check statistics in a sequential check — which, in flip, makes it extra difficult to derive legitimate and environment friendly methods of conducting sequential inference.
When extending experimentation with sequential testing from cross-sectional to longitudinal knowledge, a number of issues change. Here, we dig into two essential facets:
- The psychological swap from “metrics” to “models”
- The challenges of compressing knowledge to scale consequence calculations throughout 1000’s of experiments
The psychological swap from “metrics” to “models”
When diving into the longitudinal knowledge literature, it’s clear that the present view of metrics within the on-line experimentation neighborhood is inadequate.
In the case of a single statement per unit, it’s typically potential to have the identical “metric” (e.g., a imply or sum of some side of a unit) in a dashboard as in an experiment. We can use the difference-in-means estimator to estimate the common remedy impact, and there’s a easy and exquisite mapping between the change in our experiment and the anticipated shift within the dashboard metric if we roll out the A/B-tested expertise to the inhabitants.
In the case of longitudinal knowledge with a number of observations per unit, this mapping is far tougher to attain. The open-ended metric may be a pure metric for some, nevertheless it’s not apparent how open-ended metrics map to any metric you’ll put in a dashboard. As we confirmed in Part 1 of this sequence, the open-ended metric is a perform of the inflow to the experiment, which could even be a perform of the experiment’s design (reasonably than, for instance, the pure exercise of customers).
We discover that it’s a good suggestion to easily swap mindset from “metrics” to “models” after we transfer over to the longitudinal knowledge experiments. Instead of eager about metrics and imply variations in these metrics, we take into consideration what estimands we’re thinking about, and what fashions and estimators we will use to estimate them robustly and effectively. Approaching the issue from the modeling perspective implies that we will use the wealthy literature on econometrics panel knowledge modeling and basic longitudinal knowledge modeling to assist clear up our challenges. See, for instance, the books Econometric Analysis of Cross Section and Panel Data and Applied Longitudinal Analysis.
Data compression and enough statistics
When coping with thousands and thousands and even a whole bunch of thousands and thousands of customers in a pattern, it’s inconvenient to deal with uncooked (e.g., per unit or per measurement) knowledge in reminiscence on the machine performing the statistical evaluation. Instead, on-line experimenters with massive samples let knowledge pipelines produce abstract statistics that include the data wanted for the evaluation. In statistics, the data from the uncooked knowledge wanted for an estimator is known as “sufficient statistics”, i.e., a set of abstract statistics which are enough for acquiring the estimator in query.
For the traditional difference-in-means estimators, the enough statistics per remedy group are the sum, the sum of squares, and the depend of the result metric. For sequential testing, no extra info is usually wanted. This implies that, whatever the pattern dimension, the evaluation a part of the platform solely must deal with three numbers for every group and intermittent evaluation. In different phrases, the dimensions grows linearly within the variety of analyses.
With longitudinal knowledge fashions, extra consideration is required for the within-unit covariance construction. For many fashions and estimators, the within-unit covariance matrix must be estimated or not less than corrected for. Let Okay be the max variety of measurements per particular person within the pattern. Then estimating the covariance matrix implies that Okay*(Okay+1)/2 parameters should be estimated. In different phrases, the variety of enough statistics is rising quadratically in Okay.
There are many classical statistical fashions that can be utilized for sequential testing of parameters with rising longitudinal knowledge. However, for a lot of of these, the flexibility to compress the uncooked knowledge earlier than doing the evaluation is proscribed — which makes their sensible applicability questionable. For a pleasant introduction on knowledge compression for linear fashions, see Wong et al. (2021).
Open-ended metrics, as outlined in Part 1, are difficult from a sequential testing perspective. As we mentioned within the earlier part, to conduct a sequential check, we have to account for the covariance construction of the check statistics throughout the intermittent analyses. We will now widen our scope from open-ended metrics and discuss methods to use all out there knowledge in any respect intermittent analyses. The major argument of utilizing open-ended metrics is that they permit for precisely that, however as we’ll present, there are a lot of different methods to estimate remedy results utilizing all out there knowledge.
Formulating what to check actually comes all the way down to trade-offs between ease of derivation and implementation of sequential exams, which inhabitants remedy impact we purpose to estimate, and the effectivity of the estimator.
How to mannequin remedy results with longitudinal knowledge
Since the information going into open-ended metrics is solely bizarre panel knowledge, we will strategy the sequential testing from that perspective. There are some ways to mannequin and estimate parameters of curiosity from longitudinal knowledge. It’s useful for our dialogue to think about the next easy mannequin:
Here, is the unit i at measurement t below remedy d. The parameter
is the distinction between remedy and management. Depending on our estimation technique, the estimand that we estimate with this parameter will differ.
In precept, there are two methods of going about longitudinal knowledge modeling:
- Use commonplace cross-sectional fashions for the purpose estimate, and use cluster-robust commonplace errors to cope with the within-unit dependency. This contains, for instance, bizarre least squares (OLS) and weighted least squares (WLS) with strong standard-error estimators.
- Use a mannequin that explicitly fashions the dependency construction as a part of the mannequin, for instance, generalized least squares (GLS) and the tactic of generalized estimating equations (GEE).
To make this concrete, we take into account the next three estimators for the mannequin above.
- ROB-OLS: Estimating
with OLS and utilizing cluster-robust commonplace errors
- ROB-WLS: Estimating
with WLS and utilizing cluster-robust commonplace errors
- GLS:
with GLS (assuming the covariance construction is thought or estimated as unstructured)
This checklist of estimators is certainly not exhaustive and was chosen for illustrative functions. The major variations between these estimators are that, first, they provide completely different weights to completely different items and measurements within the level estimate and, second, they provide completely different commonplace errors and subsequently have completely different effectivity. Next, we glance nearer on the weights.
Weights of items and measurements
We return to the small instance dataset from Part 1 of this sequence, in Figure 1, under. We assume knowledge is delivered in batches. For instance, this may very well be day by day measurements being delivered after every day has handed. In this instance, the noticed cumulative samples on the three first batches are as follows:

Here, when the third batch has are available in, the primary and second items are noticed 3 times, whereas the third and fourth items are noticed twice, and the fifth and sixth items are noticed solely as soon as. As a easy however illustrative data-generating course of, we assume that there’s a distinctive common remedy impact at every time level after publicity. That is, and
, thus
.
The weights for every measurement within the level estimator for the ROB-OLS estimator is 1/(whole variety of measurements in pattern) for every measurement. This in flip implies that the purpose estimator has the anticipated worth
For the ROB-WLS, the weights could be chosen by the analyst. Interestingly, by choosing the weights for every unit to be 1/(variety of noticed measurements for the unit), the WLS estimate is an identical to the difference-in-means estimate on the open-ended metrics with a within-unit imply aggregation. The anticipated worth per intermittent analyses for this case is proven in Part 1. We repeat them right here for completeness. For the primary evaluation, the anticipated worth of the estimator is
At the second evaluation, the anticipated worth of the estimator is
And, lastly,
It is, after all, additionally potential to pick every other weights with WLS.
GLS is completely different from the OLS and WLS approaches in that it explicitly fashions the dependency, as an alternative of correcting the usual error afterward. This additionally implies that the weights within the anticipated worth are capabilities of the covariance construction. For the sake of illustration, we assume a easy fixed pairwise correlation over time throughout the three measurements within the pattern in order that the covariance matrix of the potential outcomes on the three first time intervals after publicity is given by
The anticipated values of the GLS estimator with a recognized covariance matrix is then
and
the place
We can see that when the within-unit covariance is 0, the weights coincide with the OLS weights, and when the within-unit covariance is 1, the weights coincide with the open-ended metric weights. GLS mechanically balances between the 2 primarily based on the covariance.
In abstract, there are a lot of methods to assemble treatment-effect estimators by way of longitudinal fashions. Different fashions and estimators result in completely different weightings of various measurements. In our instance, we assume that the remedy impact is equal for all items however completely different over time, which is, after all, not typically true. Perhaps the remedy impact is fixed over time. There may also be different elements affecting the remedy impact, just like the day of the week or the hour within the day, during which case the essential distinction thought-about right here may be too simplistic.
How to decide on an estimator
Giving recommendation about which estimator to make use of for longitudinal knowledge is just not easy. Different fashions and estimators give completely different effectivity relying on the covariance construction inside items over time. In addition, the estimation downside turns into more and more extra advanced with rising numbers of measurements over time.
In on-line experimentation at scale, the figuring out elements are probably the computational limitations together with whether or not or not the evaluation could be performed on a fairly small set of abstract statistics. We suggest anybody adopting longitudinal fashions to check a number of fashions and stability these trade-offs inside context.
At Spotify, we use group sequential exams, as mentioned in our earlier weblog submit’s comparability of sequential testing frameworks. A GST is solely a check on a multivariate vector of check statistics, the place the dependence construction between consecutive check statistics is exploited. For instance, for the usual difference-in-means estimator, the vector of check statistics over the intermittent analyses is asymptotically multivariate regular with a easy recognized covariance construction. This lets us derive marginal vital bounds that be certain that the correct quantity of alpha is spent at every intermittent evaluation.
The GST literature is remarkably basic on this sense and could be utilized in all kinds of conditions. For any vector of repeated testing the place the multivariate distribution is thought for the check statistics (typically asymptotically), we will theoretically receive the bounds taking the alpha spending perform and the dependence between the check statistics into consideration. Interestingly, this even holds for vectors of check statistics that relate to parameters from completely different fashions as described by Jeffries et al. (2018). For a complete dialogue of making use of GSTs to longitudinal knowledge fashions, see A.B. Shoben (2010).
There are a number of key properties to pay attention to when making use of GSTs to longitudinal knowledge experiments. Below, we talk about two of the most important keys for unlocking GSTs at scale in on-line experimentation.
Test statistics which have unbiased increments
As beforehand acknowledged, a GST is solely a multivariate check for which the vital bounds are discovered taking the covariance construction into consideration. Generally, discovering the bounds on the th evaluation requires fixing
There is one key property that influences how easy it’s to unravel this integral — if the increments between the check statistics are unbiased or not. If the increments between intermittent check statistics are unbiased, the -dimensional multivariate integral reduces to a univariate integral involving easy recursion. This discount in complexity makes it believable to unravel for the bounds for considerably bigger
. The distinction is so massive that it makes the distinction between a web based experiment implementation at scale being believable or not. When the evaluation request is distributed to the evaluation engine, we don’t wish to anticipate minutes to unravel this integral, nor do we wish the compute time to extend nonlinearly with
.
Luckily, the simplifying unbiased increment assumption holds for a lot of fashions. Kim and Tsiatis (2020) offers a complete overview of fashions for which the unbiased increment construction has been confirmed. This is a powerful checklist of lessons of fashions together with GLS, GLM, and GEE. There are even examples of fashions the place the variety of nuisance parameters are rising between intermittent analyses.
The mannequin mentioned above and the three estimators (ROB-OLS, ROB-WLS, and GLS) additionally fulfill the unbiased increment assumption. Proving that the unbiased increment assumption holds for these fashions is a bit of too technical for this submit — the reader is referred to Jennison and Turnbull (2000), chapter 11.
Without a longitudinal mannequin, it’s the failing unbiased increments assumption that invalidates commonplace GSTs
In Part 1 of this sequence, we mentioned the inflated false constructive charge for open-ended metrics with a difference-in-means z-statistic, analyzed with commonplace GST. Statistically, the issue with a naive software of a GST is that the statistical info is just not rising proportionally to the pattern dimension when it comes to items within the pattern. At a excessive degree, the consequence is that info doesn’t accrue in the way in which that the check assumes, implying that the dependence construction is completely different from what the check expects. At a extra technical degree, the sequence of check statistics not has increments which are unbiased, which makes the used GST invalid.
When we as an alternative body the open-ended metric downside as a longitudinal mannequin, we will leverage outcomes and concept for GSTs for longitudinal knowledge. This implies that we will now deal with the issues that induced the FPR inflation within the first place by designing the check and setting up its bounds in a manner that accurately accounts for the accrual of data. By doing so, we will deliver again the unbiased increments and use the check accurately regardless of the longitudinal nature of the information.
Note that the inflated FPR within the simulation of the primary a part of this sequence is just not inherently a GST downside — we simply used GST as an example the peeking downside 2.0. In basic, a sequential check derived below the presumption of a sure covariance construction utilized to a really completely different covariance construction might be invalid — and utilizing rising within-unit info results in extra difficult covariance constructions.
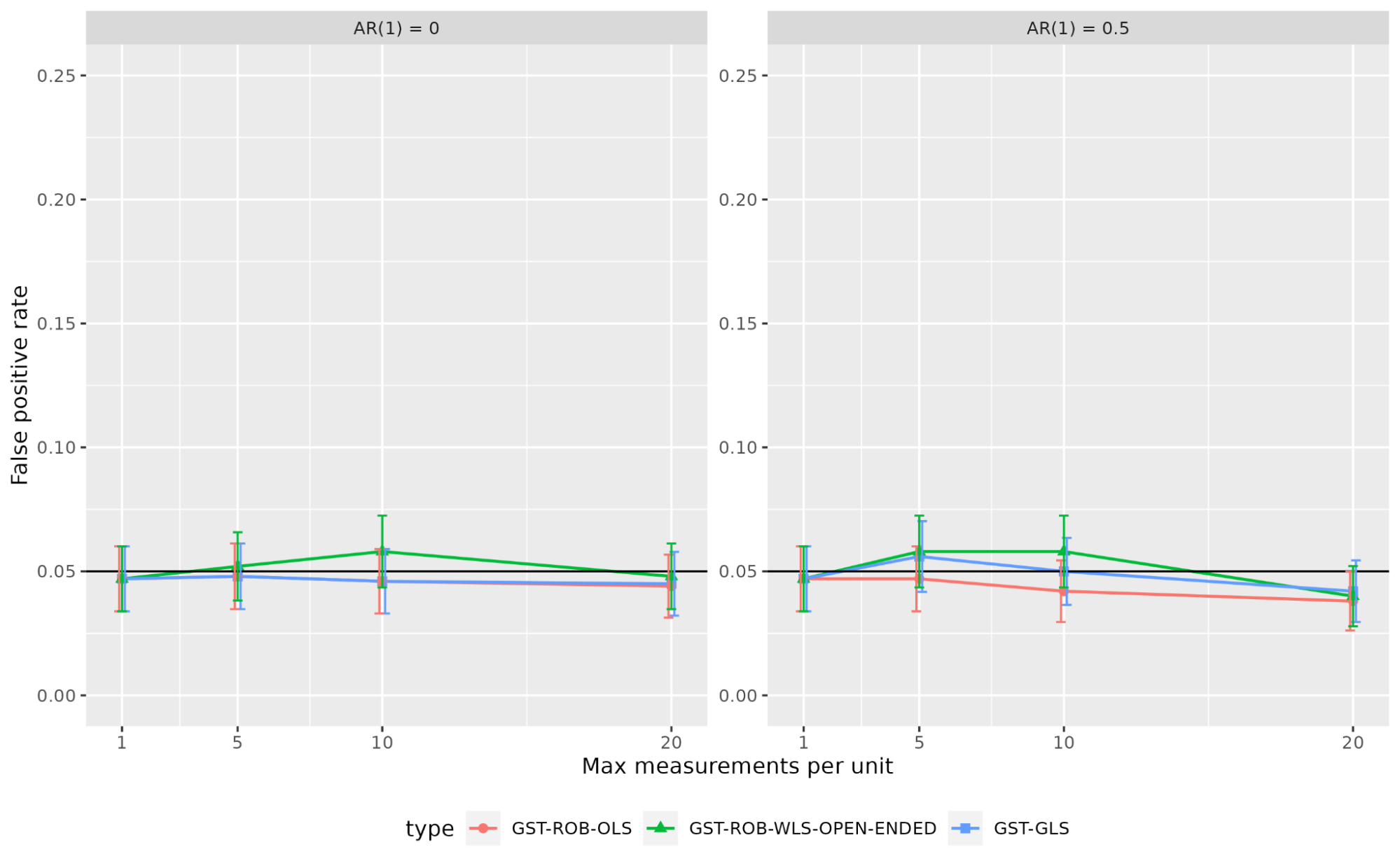
To illustrate that the three remedy impact estimators mentioned above certainly yield the meant FPRs, we performed a small simulation examine. The data-generating course of was the identical as within the simulation examine in Part 1 of this sequence. One thousand replications have been carried out per setting.
Three issues have been various within the simulation.
- Test strategies:
- GST-ROB-OLS
- GST-ROB-WLS-OPEN-ENDED
- GST-GLS
- Okay: The max variety of measurements per unit (1, 5, 10, or 20)
- AR: The coefficient of the within-unit autoregressive 1 (“AR(1)”) correlation construction (0 or 0.5)
All three strategies estimate the mannequin
however with completely different estimators. Here, GST-ROB-OLS estimates the purpose estimate with OLS and adjusts the usual errors utilizing the normal “CR0” (Liang and Zeger, 1986) estimator. GST-ROB-WLS-OPEN-ENDED estimates the purpose estimate with WLS the place the weights are chosen to recreate the open-ended metric with within-unit means and the difference-in-means level estimate. The commonplace error is once more adjusted utilizing CR0. GST-GLS is solely GLS, the place the true inside covariance matrix is handled as recognized to not require bigger samples for validity of the z-test.
Data was generated as follows. For every setting, we generated N=1,000*Okay multivariate regular observations in response to the covariance construction implied by the AR and slope parameters. We let N enhance with Okay to make sure sufficient items can be found per measurement and evaluation. In the simulation, items got here into the experiment uniformly over the primary Okay time intervals. That implies that all items have all Okay measurements noticed on the 2Okay-1th time interval, which is subsequently the variety of intermittent analyses used per replication. That is, the items that entered the experiment on time interval Okay will want Okay-1 extra days to have all Okay measurements noticed. The exams have been carried out with alpha set to 0.05.
Results
Figure 2 shows the FPR for the three strategies throughout the varied settings. As anticipated, all strategies give nominal FPR (5%) in all settings. This confirms that each one three strategies accurately alter for the within-unit covariance construction. This in turns implies that by utilizing a correct longitudinal mannequin and strong commonplace errors, we will receive a legitimate GST for open-ended metrics.
In Part 1 of this weblog submit sequence, we confirmed that utilizing commonplace sequential exams for longitudinal knowledge experiments can result in inflated false constructive charges — the peeking downside 2.0. The unique peeking downside comes from the truth that we’re utilizing a check that assumes the complete pattern is offered on the evaluation earlier than the complete pattern is offered. Peeking downside 2.0 comes from the truth that we’re utilizing a sequential check that assumes {that a} unit is absolutely noticed when coming into the evaluation earlier than all items are absolutely noticed. The mechanisms are completely different, however the consequence of an inflated false constructive charge is similar. We then identified the significance of being meticulous with the separation between measurements, metrics, estimands, and estimators when coping with sequential exams — particularly when contemplating longitudinal knowledge.
In Part 2, we mentioned what makes longitudinal knowledge completely different from cross-sectional knowledge from a sequential-testing perspective, some essential sensible implications like lacking knowledge and imbalanced panels within the estimation, and the quickly rising set of enough statistics implied by many longitudinal fashions. We then turned our consideration to the group sequential exams (GSTs) that we use at Spotify. We confirmed that the literature on GST in longitudinal knowledge settings is wealthy. We mentioned essential facets of making use of GST to longitudinal knowledge and proposed a number of estimands and estimators for which GST could be instantly utilized.
At Spotify, we’re choosing a trade-off between a wealthy sufficient mannequin for longitudinal knowledge whereas retaining the set of enough statistics moderately small. This, mixed with our quick bounds solver, makes it potential to assist environment friendly and legitimate group sequential exams whereas permitting peeking each inside and throughout items!
The authors thank Lizzie Eardley and Erik Stenberg for his or her beneficial contributions to this submit.
Tags: experimentation
[ad_2]