[ad_1]
April 06, 2023 Published by Ciarán Gilligan-Lee, Lucas Maystre

Introduction
Quantifying trigger and impact relationships is of basic significance in lots of fields, from drugs to economics. The gold normal answer to this drawback is to conduct randomised managed trials, or A/B exams. However, in lots of conditions, such trials can’t be carried out; they may very well be unethical, too costly, or simply technologically infeasible. However, even when randomised managed trials could be carried out, they normally have comparatively brief durations as a result of price issues. For instance, on-line A/B exams in business normally final for just a few weeks. This makes studying long-term causal results a really difficult process in follow, since long-term outcomes are noticed solely after an extended delay. Often short-term outcomes are completely different to long-term ones, and, as many decision-makers are fascinated by long-term outcomes, this can be a essential drawback to handle. For occasion, expertise corporations are fascinated by understanding the affect of deploying a function on long-term retention, economists are fascinated by long-term outcomes of job coaching packages, and docs have an interest within the long-term impacts of medical interventions, resembling remedies for stroke.
In distinction to experimental knowledge, observational knowledge are sometimes simpler and cheaper to accumulate, so they’re extra prone to embrace long-term end result observations. Previous work by Athey et al. [1] devised a way to estimate long-term causal results by combining observational long-term knowledge and short-term experimental knowledge. However, this technique solely works if one assumes there are no unobserved confounders within the observational knowledge. This is a robust assumption, as observational knowledge are very inclined to unmeasured confounding—which might result in severely biased causal impact estimates.
This results in the next query: can we mix these short-term experiments with observational knowledge to estimate long-term causal results when latent confounders are current?
Setting up the issue
We addressed this drawback and studied the identification and estimation of long-term causal, or therapy, results when each short-term experimental knowledge and observational knowledge with latent confounders can be found.
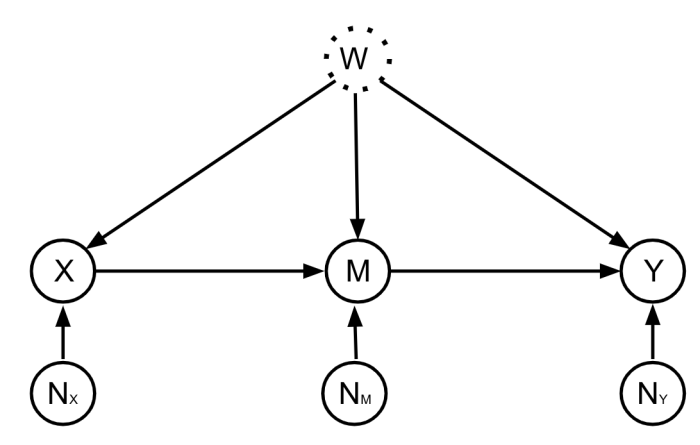
First, to formally state the query posed on the finish of the final part, we graphically illustrate the causal construction between our variables of curiosity within the above directed acyclic graph (DAG). Here, X is the therapy, M is the short-term end result, and Y is the long-term end result. We consider M as a mediator between X and Y: the causal affect of X on Y occurs not directly via M. The unobserved confounder is represented as W. The query we goal to resolve can now be formally said:
Given experimental samples between (X, M), and (historic) observational samples between (X, M, Y), can we estimate the causal impact of X on Y?
We initially work with linear structural equation fashions:
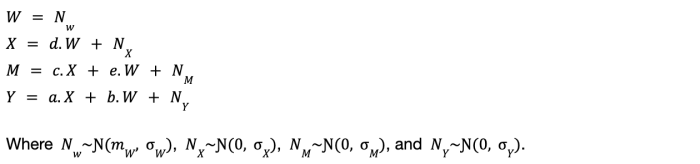
Our long-term causal impact estimator is obtained by combining regression residuals with short-term experimental knowledge in a selected method to create an instrumental variable, which is then used to quantify the long-term causal impact via instrumental variable regression.
But earlier than we dive into our full answer, allow us to attempt a heat up drawback to realize some instinct for a way we’d proceed.
Warm up drawback: a brand new estimator for the front-door causal mannequin
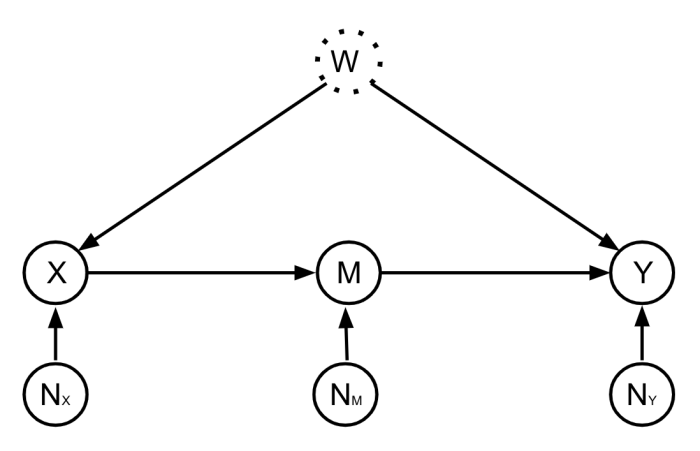
Consider the well-known front-door causal construction, illustrated within the DAG above. Notice the primary distinction between this DAG and the one from the earlier part is that W doesn’t straight trigger M within the front-door construction. In the front-door causal construction, to estimate the causal impact of X on Y from observational knowledge, the usual answer is to:
- regress M on X to get c,
- then regress Y on M and X to get a.
The causal impact is simply their product: a.c
Now, as a substitute of the usual estimation technique outlined above, let’s attempt one thing new. Estimating c as earlier than, estimate a as follows:
- Regress M on X, and compute the residual: Residual[M|X] = NM
- Use NM as an instrumental variable for M -> Y
Given the above DAG, one can see that NM is an instrumental variable for M -> Y as a result of it’s impartial of W. This realisation is kind of highly effective, because it permits us to estimate the impact of M on Y. Using NM as an instrumental variable to estimate the impact of M on Y corresponds to regressing Y on NM and M on NM and taking the ratio of the coefficients. This leads to a. In the context of the front-door causal construction, this technique gives a brand new causal estimator, which can be of impartial curiosity.
We’ll now see that this second technique to estimating a could be tailored to resolve the complete drawback when W straight causes M.
The full answer
Returning to the primary DAG and the complete drawback, we see that the residual from regressing M on X isn’t the impartial noise time period NM on this case—as a result of confounding from W. This implies that the residual is correlated with W, and isn’t an instrumental variable for M -> Y. However, utilizing the experimental samples between X and M, we will take away the confounding bias on the residual, and use this de-biased residual as an instrument for M -> Y!
That is, within the full drawback we will nonetheless assemble an instrumental variable that can be utilized to estimate the impact of M on Y within the presence of an unobserved confounder. In our paper, we show that the next variable
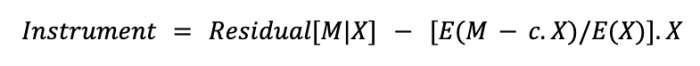
is an instrumental variable for M -> Y. Here, c is the causal impact of X on M obtained from the experimental knowledge, and E(.) is the expectation operator. In our paper, we show that the instrumental estimator utilizing this variable is unbiased, and analytically examine its variance.
We prolong this estimator from linear structural causal fashions to the partially linear structural fashions routinely studied in economics and show unbiasedness nonetheless holds beneath gentle assumptions. Finally, we empirically take a look at our long-term causal impact estimator, demonstrating correct estimation of long-term results on artificial knowledge, in addition to actual knowledge from the International Stroke Trial.
Conclusion
Our paper supplied a way to mix short-term experiments with long-run observational knowledge to estimate long-term causal results even when latent confounders are current. Although long-term impact estimation is our main focus, the estimator and strategies described could be utilized to any single-stage causal impact. In this context, they are often interpreted as a novel technique that mixes Front-Door and Instrument Variables to estimate causal results within the presence of unobserved confounders.
For full particulars, see our paper:
Estimating long-term causal results from short-term experiments and long-term observational knowledge with unobserved confounding
Graham Van Goffrier, Lucas Maystre, & Ciarán M. Gilligan-Lee
CLeaR (Causal Learning and Reasoning), 2023
References
[1] Athey, Susan, et al. The surrogate index: Combining short-term proxies to estimate long-term therapy results extra quickly and exactly. No. w26463. National Bureau of Economic Research, 2019.
[ad_2]
