[ad_1]
November 24, 2022 Published by Lucas Maystre

TL;DR: Survival evaluation offers a framework to cause about time-to-event knowledge; at Spotify, for instance, we use it to know and predict the best way customers may interact with Spotify sooner or later. In this work, we convey temporal-difference studying, a central concept in reinforcement studying, to survival evaluation. We develop a brand new algorithm that trains a survival mannequin from sequential knowledge by leveraging a temporal consistency situation, and present that it outperforms direct regression on noticed outcomes.
Survival evaluation
Survival evaluation is the department of statistics that offers with time-to-event knowledge, with functions throughout a variety of domains. Survival fashions are utilized by physicians to know sufferers’ well being outcomes. Such fashions are additionally utilized by engineers to review the reliability of units starting from laborious drives to hoover cleaners. At Spotify, we use survival fashions to know the best way customers will interact with Spotify at a later date.. Such fashions are essential to make sure that Spotify makes selections which are aligned with our customers’ long-term satisfaction—from tiny selections equivalent to algorithmic suggestions all the best way to massive modifications within the consumer interface.
Here is a typical state of affairs for survival evaluation. Suppose that we’re focused on predicting, for each Spotify consumer with a free account, the time till they convert to a Premium subscription. We name this conversion the “event”. To be taught a mannequin that predicts the time-to-event, we begin by amassing a dataset of historic observations.
- We choose a pattern of customers that have been energetic a number of months in the past, and acquire a function vector that describes how they have been utilizing Spotify again then.
- We then fast-forward to the current and verify if they’ve transformed within the meantime. For these customers who transformed, we file the time at which it occurred. Note that many customers within the pattern is not going to but have transformed, and the technical time period for these observations is “right-censored” (the time-to-event is above a given worth, however we have no idea by how a lot). These observations nonetheless carry helpful alerts in regards to the time-to-event.
With this we now have constructed a dataset of triplets (x0, t, c), one for every consumer within the pattern. We name x0 the preliminary state; it describes the consumer in the beginning of the statement window (i.e., a number of months in the past). The second amount, t, denotes the time-to-event (if the consumer has transformed for the reason that starting of the window) or the time till the top of the statement window. Finally, c is a binary indicator variable that merely denotes whether or not the consumer has transformed throughout the statement window (c = 0) or not (c = 1).
The subsequent step is to posit a mannequin for the info. One mannequin that could be very easy and common is known as the Cox proportional-hazards mannequin. At Spotify, we now have additionally had good outcomes with Beta survival fashions. Given a dataset of observations, we are able to practice a mannequin by maximizing its chance underneath the info—a typical strategy in statistics and machine studying. Once we now have educated such a mannequin, we are able to use it to make predictions about customers exterior of the coaching dataset. For instance, a amount of curiosity is
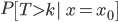
the chance {that a} consumer’s time-to-event T is bigger than ok, given the consumer’s preliminary state x0.
The dynamic setting
Increasingly, it’s changing into commonplace to gather a number of measurements over time. That is, as a substitute of solely gaining access to some preliminary state x0, we are able to additionally get hold of extra measurements x1, x2, … collected at common intervals in time (say, each month). To proceed with our instance, we observe not simply how lengthy it takes till a free consumer converts but in addition how their utilization evolves over time. In medical functions, from an preliminary state indicating, for example, options of a affected person and a alternative of medical therapy, we would observe not simply the survival time however wealthy data on the evolution of their well being.
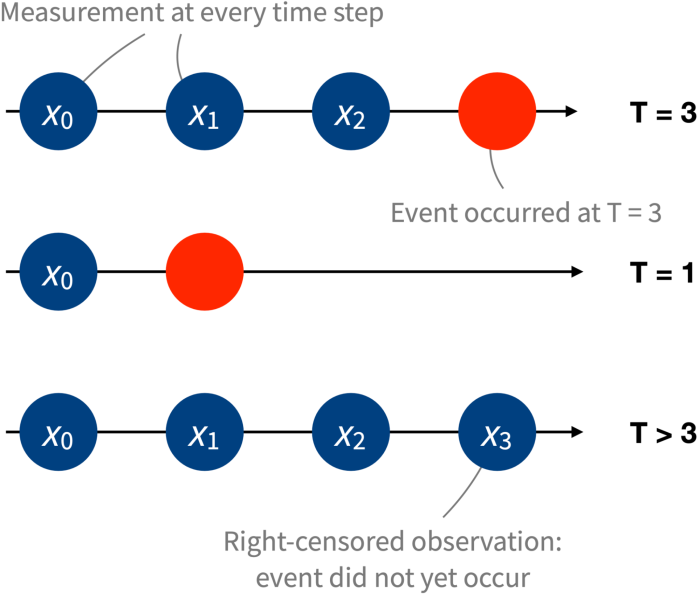
In this dynamic setting, the info encompass sequences of states as a substitute of a single, static vector of covariates. This naturally raises the query: Can we reap the benefits of sequential knowledge to enhance survival predictions?
One strategy to doing so is known as landmarking. The concept is that we are able to decompose sequences into a number of easier observations. For instance, a sequence that goes by means of states x0 and x1 after which reaches the occasion could be transformed into two observations: one with preliminary state x0 and time-to-event t = 2, and one other one with preliminary state x1 and time-to-event t = 1.
This is neat, however we propose that we are able to do even higher: we are able to reap the benefits of predictable dynamics within the sequences of states. For instance, if we all know very effectively what the time-to-event from x1 is like, we would acquire rather a lot by contemplating how seemingly it’s to transition from x0 to x1, as a substitute of attempting to be taught in regards to the time-to-event from x0 straight.
A detour: temporal-difference studying
In our journey to formalizing this concept, we take just a little detour by means of reinforcement studying (RL). We think about the Markov reward course of, a formalism regularly used within the RL literature. For our functions, we are able to consider this course of as producing sequences of states and rewards (actual numbers): x0, r1, x1, r2, x2, … A key amount of curiosity is the so-called worth perform, which represented the anticipated discounted sum of future rewards from a given state:
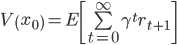
the place γ is a reduction issue. Given sequences of states and rewards, how will we estimate the worth perform? A pure strategy is to make use of supervised studying to coach a mannequin on a dataset of empirical observations mapping a state x0 to the discounted return
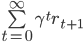
In the RL literature, that is referred to as the Monte Carlo technique.
There is one other strategy to studying the worth perform. We begin by making the most of the Markov property and rewrite the worth perform as
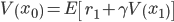
This can be referred to as the Bellman equation. This suggests a distinct method to make use of supervised studying to be taught a worth perform: as a substitute of defining the regression goal because the precise, noticed discounted return, outline it because the noticed speedy reward r1, plus a prediction on the subsequent state, γV(x1), the place the worth at x1 is given by a mannequin. This may appear to be round reasoning (utilizing a mannequin to be taught a mannequin!), however in reality this concept is central in reinforcement studying. It is understood underneath the title of temporal-difference studying, and has been a key ingredient within the success of RL functions over the previous 30 years.
Our proposal: temporally-consistent survival regression
We now return to our dynamic survival evaluation setting, and to the issue of predicting time-to-event. Is there one thing we are able to be taught from temporal-difference studying in Markov reward processes? On the one hand, there isn’t a notion of reward, low cost issue or worth perform in survival evaluation, so at first sight it’d appear to be we’re coping with one thing very completely different. On the opposite hand, we’re additionally coping with sequences of states, so perhaps there are some similarities in spite of everything.
A vital perception is the next. If we assume that the sequence of states x0, x1, … kind a Markov chain, then we are able to rewrite the the survival chance as
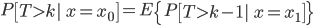
for any ok ≥ 1. Intuitively, this identification states that the survival chance at a given state must be related (on common) to the survival chance on the subsequent state, accounting for the delay. This appears similar to the Bellman equation above. Indeed, in each circumstances, we reap the benefits of a notion of temporal consistency to write down a amount of curiosity (the worth perform or the survival chance) recursively, by way of a right away statement and a prediction on the subsequent state.
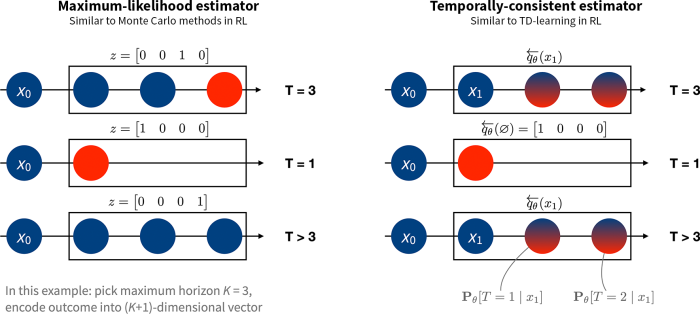
Building on this perception, we develop algorithms that mirror temporal-difference studying, however within the context of estimating a survival mannequin. Instead of utilizing the noticed time-to-event (or time to censoring) because the goal, we assemble a “pseudo-target” that mixes the one-hop consequence (whether or not the occasion occurs on the subsequent step or not) and a prediction about survival on the subsequent state. This distinction is illustrated within the determine under.
Benefits of our algorithm
Our strategy could be considerably extra data-efficient than maximum-likelihood-style direct regression. That is, our algorithm is ready to decide up delicate alerts which are predictive of survival even when the scale of the dataset is restricted. This results in predictive fashions which are extra correct, as measured by a number of efficiency metrics. We show these advantages in two methods.
First, we handcraft a process that highlights a setting the place our algorithm yields monumental positive factors. In quick, we design an issue the place it’s a lot simpler to foretell survival from an preliminary state by making the most of predictions at intermediate states, as these intermediate states are shared throughout many sequences (and thus survival from these intermediate states is far simpler to be taught precisely). We name this the data-pooling profit, and our strategy efficiently takes benefit of this. The take-away is that implementing temporal-consistency reduces the impact of the noise contained within the noticed time-to-event outcomes.
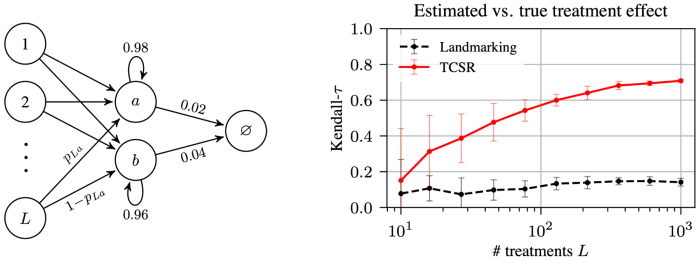
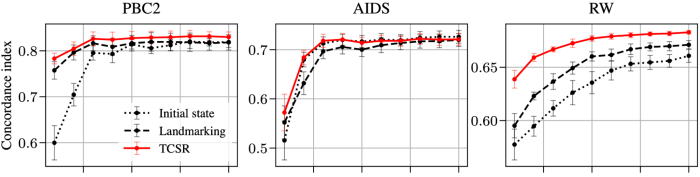
Second, we consider fashions realized utilizing our algorithm empirically on real-world datasets. To facilitate reproducibility, we give attention to publicly accessible medical datasets, recording survival outcomes of sufferers recognized with an sickness. For every affected person, biomarkers are recorded at examine entry and at common follow-up visits. In addition, we additionally think about an artificial dataset. In every case, we measure a mannequin’s predictive efficiency as a perform of the variety of coaching samples. Models educated utilizing our strategy systematically end in higher predictions, and the distinction is especially robust when the variety of samples is low. In the determine under, we report the concordance index, a well-liked metric to judge survival predictions (greater is best).
A bridge between RL and survival evaluation
Our paper focuses totally on utilizing concepts from temporal-difference studying in RL to enhance the estimation of survival fashions. Beyond this, we additionally hope to construct a bridge between the RL and survival evaluation communities. To the survival evaluation group, we convey temporal-difference studying, a central concept in RL. Conversely, to the RL group, we convey many years of modeling insights from survival evaluation. We assume that some RL issues could be naturally expressed by way of time-to-event (for instance, maximizing the size of a session in a recommender system), and we hope that this bridge can be helpful. In the paper, we briefly sketch how our strategy may very well be prolonged to issues with actions, paving the best way for RL algorithms tailor-made to survival settings.
If you have an interest in getting hands-on with this, we encourage you to take a look at our companion repository, which incorporates a reference Python implementation of the algorithms we describe within the paper. For extra data, please discuss with our paper:
Temporally-Consistent Survival Analysis
Lucas Maystre and Daniel Russo
NeurIPS 2022
[ad_2]
