Bringing Sequential Testing to Experiments with Longitudinal Data (Part 1): The Peeking Problem 2.0

July 18, 2023

Published by Sebastian Ankargren (Sr. Data Scientist), Mattias Frånberg (Sr. Data Scientist), and Mårten Schultzberg (Sr. Manager/Staff Data Scientist)

At Spotify, we’re consistently bettering our information infrastructure, which implies we will get suggestions on experiments earlier and earlier. To enable for early suggestions in a risk-managed method, we use sequential assessments to observe regressions within the experiments. However, when shifting towards smaller and smaller time home windows, we’re confronted with a number of measurements per unit in our evaluation, which is named longitudinal information. This, in flip, introduces new challenges for designing sequential assessments. While papers like Guo and Deng (2015) and Ham et al. (2023) focus on such a information and its use in experimentation, the challenges we current haven’t to one of the best of our information been absolutely addressed within the on-line experimentation neighborhood. Our method to addressing these challenges is offered in two elements:  

Part 1: The peeking downside 2.0 and different challenges that happen when making use of normal sequential assessments within the presence of a number of observations per unit 

Part 2 (coming quickly): General recommendation for performing sequential assessments within the presence of a number of observations per unit, and the way Spotify makes use of group sequential assessments (GSTs) for a big class of estimators

Continuous monitoring of A/B assessments is an integral a part of on-line experimentation. Sequential testing, though launched in statistics and utilized in medical trials for over 70 years (Wald, 1945), was not broadly adopted within the on-line experimentation neighborhood till it was popularized by papers like Johari et al. (2017) and others. The normal “peeking problem” happens when individuals working an experiment conduct statistical evaluation on the pattern earlier than all members’ outcomes have been noticed, which results in an inflation of the false optimistic threat (Johari et al. 2017) and violates the statistical assumptions of the take a look at. 

Sequential testing provides an answer to the peeking downside because it allows peeking through the experiment with out inflating the false optimistic price (FPR). There is now a wealthy literature on sequential testing. For a complete overview and comparability of various sequential testing frameworks, see our earlier weblog submit. 

However, we’ve noticed a brand new downside, which we name the “peeking problem 2.0” — an issue that may considerably inflate false optimistic charges regardless of using sequential assessments. This downside is related for information the place every participant is measured at a number of deadlines through the experiment, and it will probably happen when a participant’s outcomes are peeked at earlier than all of the measurements of that participant have been collected (“within-unit peeking”). 

To illustrate the challenges that come up with longitudinal information, we are going to examine the next two widespread varieties of metrics:

1. Cohort-based metrics. Where items are measured over the identical, mounted time window after being uncovered to the experiment. These metrics don’t undergo from the peeking downside 2.0. However, these metrics pressure the experimenter to both wait longer for outcomes or use much less of the obtainable information. 
2. Open-ended metrics. Where metrics are based mostly on all obtainable information per unit. These metrics are extremely prone to be affected by the peeking downside 2.0 as a result of normal sequential assessments are sometimes invalid. However, they’re interesting as a result of they at all times make the most of all obtainable information. Open-ended metrics are widespread in follow and supported by a number of on-line experimentation distributors. 

To allow an in depth dialogue, we first focus on the must be exact with the underlying statistical objective. When a number of measurements can be found per unit, it turns into extra necessary to be clear on which kind of therapy impact we’re attempting to find out about. Then, we give an outline of cohort-based metrics and open-ended metrics, focus on their trade-offs, and clarify why an open-ended metric poses particular challenges for sequential statistical evaluation. By conducting a small Monte Carlo simulation examine, we present that utilizing normal sequential assessments for open-ended metrics can result in considerably inflated false optimistic charges. 

Longitudinal information and when to measure outcomes

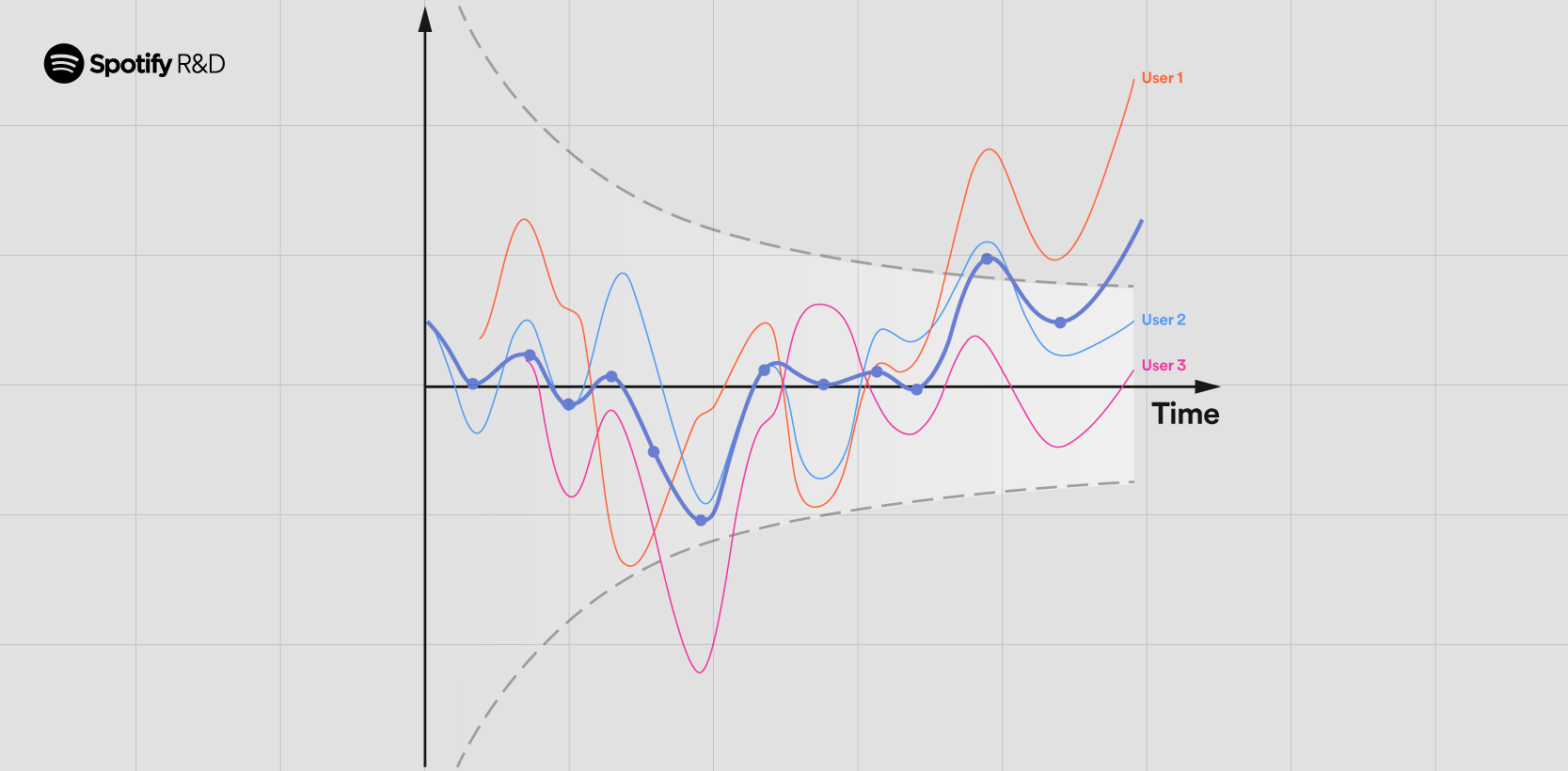
Although the event of infrastructure for gathering information has made enormous strides ahead, this has not been mirrored within the literature on sequential testing. This growth has made it potential to measure items and combination outcomes extra regularly through the experiment. Interestingly, regardless that the literature on sequential testing is closely targeted on the flexibility to constantly monitor outcomes throughout experiments, there was little dialogue about how one can incorporate extra granular measurements in sequential assessments in a sound method. For instance, to know how a lot audio content material a Spotify person consumes — and assuming a person wants time to pay attention — measuring the distinction in music consumption throughout the first 5 seconds wouldn’t yield distinguishable outcomes. The person wouldn’t have had the time to train their doubtlessly modified habits underneath the therapy. In different phrases, with out having the ability to incorporate repeated measurements per unit within the experiment evaluation, small time-window measurements inevitably create a battle between early detection and using all the information obtainable for a unit. So ought to we measure items (e.g., customers or prospects) for a really quick time after they enter the experiment in order that the take a look at will be carried out early, or ought to the unit be measured for an extended time window in order that we study extra in regards to the unit’s response? The solely solution to have the cake and eat it too is to think about repeated measurements per unit within the sequential evaluation. 

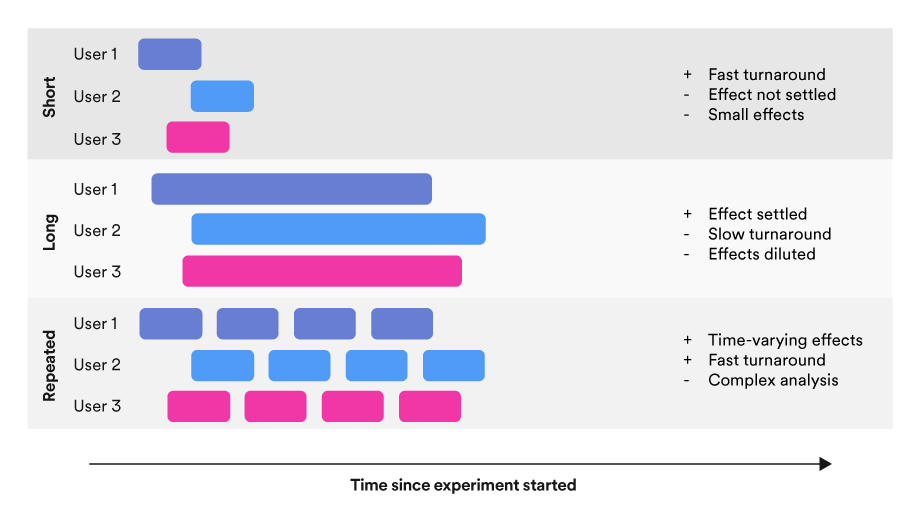
Figure 1 shows completely different information assortment patterns. Each field represents one remark made obtainable for evaluation the place the corresponding field ends. The Short and Long panels file just one remark per unit, the place the distinction is the time window wherein the remark is calculated. This aggregation into just one remark implies a trade-off between getting a measurement quick versus observing the unit for lengthy sufficient. In the repeated panel, all measurements per unit are used as observations, and there’s no trade-off between the 2. However, statistical evaluation of panels of repeated measurements per unit (i.e., longitudinal information) is extra advanced.

Separating the ideas makes it simpler to resolve the issue

It’s straightforward to confuse metrics on the one hand, and estimands and statistical assessments concerning them on the opposite. However, to derive legitimate and environment friendly sequential assessments in additional common information settings, we discover that it’s essential to separate between two necessary questions:

1. What habits or side might be measured per unit, and the way typically and over what time home windows will this be measured?
2. What therapy impact, estimator, and statistical assessments might be used to guage if the therapy is performing higher than the management?

Many on-line experimenters are so used to working with common therapy results and normal difference-in-means estimators that the measurements, the metric, the estimand, the estimator, and the statistical take a look at are all conflated. To make this concrete, take into account the next instance: say that we’re testing a change for which the choice speculation is that music consumption will enhance. The final result is measured utilizing the metric “average minutes played over a week”, which is a typical metric at Spotify. This metric relies on a single remark per person, their complete minutes performed over per week, which, in flip, relies on extra granular measurements. These extra granular measurements are sometimes hourly or day by day.

It’s normal follow to match the difference-in-means between the therapy and management group. This is the place the chance of conflation of ideas begins to extend. The difference-in-means estimator is commonly an unbiased estimator of the typical therapy impact on the metric in query. However, there are lots of unbiased estimators for the typical therapy impact on any given metric. A standard various to the difference-in-means estimator is the covariate-adjusted regression estimator — of which CUPED (Deng et al. 2013) is a particular case. For many estimators, there are additionally a number of potential statistical inference strategies. For each the difference-in-means estimator and the covariate-adjusted estimator, there are lots of methods to conduct inference, e.g., asymptotic regular concept–based mostly t- and z-tests, randomization inference, or bootstrap. There are, after all, many different fascinating estimands for any given metric, for instance, the difference-in-median. Additionally, it is perhaps preferable for a similar set of measurements to make use of group-level aggregated metrics — typically referred to as ratio metrics and click-through price metrics — the place no within-unit aggregation throughout measurements is carried out. 

When extending sequential testing to longitudinal information settings, it turns into more and more necessary to be clear in regards to the separation of measurements, metrics, estimands, estimators, and inference.

The information and statistical objective of a web based experiment

In probably the most fundamental of experiments, the objective is to evaluate whether or not a therapy is “better” than a management. By randomly distributing items — comparable to customers — to both therapy or management, the one distinction between items within the two teams is which expertise they’ve been randomly allotted to. The randomization permits us to causally declare that any distinction that we see between the 2 teams in metrics is due to the therapy. To extra clearly see how we formulate the distinction, or in what sense therapy is healthier than management, we have to introduce some notation.

To make the statistical challenges exact, we leverage the framework of potential outcomes. We denote by the th potential final result underneath therapy for unit . The distinction represents the person therapy impact for unit at time . We let 

denote the noticed potential final result for unit at time . This could possibly be, for instance, music consumption throughout a day or variety of app crashes throughout an hour on the th measurement after the unit was uncovered to both therapy () or management (). During the information assortment of an experiment, the sequence of noticed measurements will sometimes be a mixture of repeated measurements of customers which have already been noticed at the least as soon as, and the primary measurement of latest customers. 

To illustrate some particulars and ideas, take into account the next instance of a small pattern. We assume information is delivered in batches. For instance, this could possibly be day by day measurements being delivered after every day has handed. In this instance, the noticed samples of the three first batches are proven in Figure 2.

Here, when the third batch has are available, the primary and second items are noticed thrice, whereas the third and fourth items are solely noticed twice, and the fifth and sixth items are noticed solely as soon as. When samples of measurements like this can be found, there are lots of choices obtainable for testing the distinction between therapy and management. 

Cohort-based and open-ended metrics are two widespread methods of aggregating information

The phrases “cohort-based metrics” and “open-ended metrics” are typically casually used to explain two distinct varieties of metrics. These should not the one varieties of metrics and are arguably in themselves inflicting conflation of statistical ideas, as mentioned above. However, they function a wonderful instrument for illustrating the trade-offs and challenges of working with longitudinal information in a sequential testing setting, and we outline them subsequent.

Cohort-based metrics

A cohort-based metric is centered across the idea of time since publicity (TSE). For instance, at Spotify, we depend on days since publicity and outline metrics comparable to “average minutes played during the first seven days of exposure”. For this metric, solely customers with at the least seven days of publicity have a worth for this measurement. This implies that the information from customers with six or fewer days of publicity at a given intermittent evaluation is excluded from that evaluation. All measurements collected for customers after their seventh day of publicity are additionally discarded from the calculation of the metric. Moreover, the primary evaluation can’t be accomplished till seven days into the experiment, and at that time it’s going to solely be the items that got here into the experiment the primary day which can be included within the evaluation. 

Let’s make this a bit extra exact. A cohort-based metric is outlined for mounted home windows of measurements in relation to the time since publicity. For instance, Figure 3 shows the obtainable information for a given person, the place the containers signify day by day information factors.

An instance of a cohort-based metric could possibly be the typical throughout customers of the entire throughout days 3 and 4. In this case, the person within the instance would contribute with the measurement 12+16=28 on day 4, and wouldn’t have been measured previous to day 4. Later information factors should not used, and the person’s measurement, 28, stays mounted. The metric may use different types of aggregations — the first function of the cohort-based metric is that every unit comes into the evaluation with one remark, and that remark is mounted between analyses.

Let’s now return to the sooner small instance dataset with three batches. Define the metric as the typical over the primary two measurements after publicity. With the given noticed measurements, the cohort-based metric wouldn’t be outlined for any items when solely the primary batch is noticed. At the second batch, the pattern by way of the metric could be

the place measurements are discarded. When the third batch is available in, we’ve got

the place measurements are discarded.

Let’s now examine the difference-in-means estimator on this metric. For the primary batch, once more, there aren’t any items with noticed metrics. When the second batch is available in, the estimator might be

At the third batch, we’ve got

For the comparability to open-ended metrics beneath, word that, for any given cohort-based metric, the estimator at any given intermittent evaluation yields an unbiased estimator of the identical estimand. Let’s assume for simplicity that and , thus the typical therapy impact follows the sample . That is, therapy results are equal throughout items, however completely different over time. The anticipated worth of the estimator on the first potential evaluation is

.

For the second evaluation, we’ve got

.

That is, at any intermittent evaluation the place the metric is outlined for some items, the estimator is an unbiased estimator of the typical therapy impact throughout the 2 first measurements after publicity.

The enforced trade-off between early detection and information utilization

For cohort-based metrics, the experimenter wants to decide on between early detection and information utilization. That is, if the cohort-based metric is outlined over many measurements, items won’t have any metric values till they’ve at the least that many measurements noticed. At the identical time, if the cohort-based metric is outlined over solely, say, the primary measurements, all measurements noticed after that might be discarded for every unit. It is feasible to outline a number of cohort-based metrics, one for every days-since-exposure offset, however then the evaluation might want to account for a number of testing with diminished sensitivity as a consequence. 

Open-ended metrics

An various to a cohort-based metric is an open-ended metric. With an open-ended metric, all obtainable information is used at every evaluation time. In follow this may imply various things, for instance, the typical therapy impact on the within-unit combination, or the median therapy impact on the typical day by day consumption throughout items and days, and so on. In most instances, an “open-ended” metric is similar to a cohort-based metric. The foremost distinction is that, no matter aggregation perform, the metric is outlined per unit from when the primary measurement is noticed per unit, and all measurements after which can be included (therefore “open-ended”). 

Consider once more the hypothetical information from Figure 3. With an open-ended metric based mostly on within-user averages, this person would contribute the measurement 15/1 on the primary day; on the second day, their contribution could be (15+10)/2; on the third day, it might be (15+10+12)/3; and so forth. With an open-ended metric, items are measured as quickly as potential, and all obtainable information is used.

Open-ended metrics should not unusual in follow, and so they’re supported by a number of industrial on-line experimentation distributors. Open-ended metrics are interesting as a result of they will leverage all the obtainable information at any given time limit and seem much like metrics utilized in dashboards and stories. However, as we are going to see within the subsequent part, that similarity hinges on sturdy assumptions which can be unlikely to be met in follow. 

The shifting goal of open-ended metrics makes (sequential) statistical inference difficult

An necessary distinction between open-ended metrics and cohort-based metrics is that, for open-ended metrics, the measurement for a given unit modifications between intermittent analyses. This implies that any estimator based mostly on a metric on prime of those measurements will fluctuate between intermittent analyses for 2 causes: each attributable to new items getting into the experiment and as a result of new measurements turn into obtainable for already noticed items, thereby updating every unit’s “measurement”. This poses a significant problem for deriving legitimate sequential assessments.  

Furthermore, the difference-in-means estimator on an open-ended metric is tough to interpret as a result of the inhabitants parameter for which it’s an unbiased estimator is altering between intermittent analyses. We once more return to the small instance dataset with three batches. The difference-in-means estimator on the open-ended metric with the within-unit imply because the aggregation perform could be

Using the identical imply and therapy construction as for the cohort-based instance, for the open-ended metric, the anticipated worth of the estimator on the first evaluation is

At the second evaluation, the anticipated worth of the estimator is

And, lastly,

.

As we will see, the implied estimand modifications between analyses for open-ended metrics, which stands in distinction to cohort-based metrics. Due to the within-unit means altering between intermittent analyses, the estimand turns into an more and more extra difficult weighted sum of the three first-time therapy results. In follow, the weights might be a perform of the consumption distribution, which normally is an arbitrary solution to choose the weights — particularly if ramp-up or different gradual schemes for rising the attain of the experiment are used. 

One problem with the altering estimand is that normal sequential assessments are sometimes derived for a set parameter of curiosity. Since open-ended metrics suggest an estimand which will change from evaluation to evaluation, extra care must be taken when deriving sequential assessments. Using normal sequential assessments can result in severely inflated FPRs. 

A small Monte Carlo examine

To illustrate the potential FPR inflation from utilizing the open-ended metric method within the presence of longitudinal information, we conduct a small simulation examine.

 As a benchmark, we embrace treating the measurements inside and throughout items as all impartial and identically distributed. This is a naive method, which might be incorrect by development if the within-unit correlation is non-zero. We carry out 1,000 replications per setting.  

We fluctuate two parameters within the simulation design:

• Okay: The max variety of measurements per unit is ready to Okay=1, 5, 10, 20.
• AR(1): The coefficient of the within-unit autoregressive correlation construction is ready to 0 and 0.5.

Data is generated as follows. For every simulation design, we generate N=1,000*Okay multivariate regular observations with a within-unit correlation construction given by an AR(1) course of with the given parameter worth. We let N enhance with Okay to make sure sufficient items can be found per measurement and evaluation. In the simulation, items come into the experiment uniformly over the primary Okay time intervals, which implies that all items can have all Okay measurements noticed on the 2Okay-1th time interval, which is, due to this fact, the variety of intermittent analyses used per replication. That is, the items that entered the experiment at time interval Okay will want Okay-1 extra days to have all Okay measurements noticed. The assessments are carried out with alpha set to 0.05.        

In the simulation, we examine three strategies:

1. IID: Standard GST, treating every measurement inside and between items as IID. The anticipated pattern measurement is ready to N*Okay.
2. Open-ended Metric: Standard GST, utilized to the open metric as outlined above. The experiment ends when the final items have their first measurements noticed. This implies that not each unit reaches their max variety of measurements.
3. Open-ended Metric (oversampled): Same as Open-ended Metric, however the experiment is sustained till all items have all Okay measurements noticed. 

We embrace each “Open-ended Metrics” and “Open-ended Metrics (oversampled)” for example that there are a number of mechanisms at play that drive the false optimistic inflation. When implementing these assessments, it instantly turns into clear how awkward it’s to make use of normal sequential assessments for open-ended metrics. For a typical GST, the complete pattern (by way of variety of items) is collected as quickly because the final unit has gotten its first measurement noticed. This implies that all alpha is spent already on the Okayth evaluation, after which the take a look at statistic nonetheless updates attributable to new measurements coming in implying extra Okay-1 analyses. This inevitably results in an inflated FPR. This is along with the inflated FPR that happens as a result of unmodeled covariance inside items.

Results

Figure 4 shows the outcomes. The x axis is the utmost variety of repeated measurements per unit. The y axis is the empirical false optimistic price. The colours correspond to 3 strategies: 1) IID treating all measurements throughout items and time factors as IID; 2) OM utilizing a within-unit imply open-ended metric stopping consumption as soon as all items have at the least one measurement; and three) OM (oversampled), which is identical as OM, however information assortment continues till all items have all measurements. The bars point out 95% normal-approximation confidence intervals for the true false optimistic price. The two panels show the outcomes for the three strategies underneath every correlation construction, respectively. For each settings, once we solely have one measurement per particular person, the pattern is just the N IID remark being analyzed as soon as. That is, the GST reduces to fixed-horizon assessments, and all variants ought to have nominal alpha ranges.

In the IID case, when the within-unit measurements are impartial (AR(1)=0) the FPR is centered on alpha throughout numbers of measurements. Using the IID technique, as quickly because the within-unit correlation over time is nonzero, the false optimistic inflation will increase accordingly. 

For the 2 open-ended metric strategies, the false optimistic price inflates because the variety of measurements per unit will increase. As anticipated, the FPR is greater within the oversampled case, but it surely solely explains a small portion of the FPR inflation. Here, the sample is considerably reverse to the IID case, in that the upper the within-unit autocorrelation, the much less inflated the FPR. This is predicted, as when the within-correlation will increase, the quantity of latest info within the within-unit imply from a brand new remark goes down. If the within-unit correlation approaches 1, the open-ended metric wouldn’t fluctuate inside items over time, and thus the peeking downside 2.0 wouldn’t happen. 

In abstract, with out taking the within-unit covariance under consideration, there’s a excessive threat that we are going to find yourself inflating the FPR, regardless of utilizing sequential assessments. While we targeted on GSTs within the simulation right here, the identical downside can happen in different households of sequential assessments that don’t account for the within-unit covariance. Due to the peeking downside 2.0, we can’t anticipate ensures on false optimistic charges to carry except we modify the sequential take a look at accordingly. 

Conclusion

More frequent measurements allow quicker suggestions in on-line experiments. However, extra frequent measurements suggest repeated measurements per unit, a kind of information referred to as  longitudinal information. In phrases of sequential testing, shifting from a single remark per unit to repeated observations per unit introduces new challenges. In this submit, we’ve got proven that with out addressing the possibly extra advanced covariance construction of the estimator between intermittent analyses, the false optimistic price will be severely inflated. This is brought on by the peeking downside 2.0 — peeking on items’ outcomes earlier than all their measurements are noticed.

The unique peeking downside stems from the truth that we’re utilizing a take a look at that assumes the complete pattern is out there on the evaluation earlier than the complete pattern is out there. The peeking downside 2.0, however, stems from the truth that we’re utilizing a sequential take a look at that assumes {that a} unit’s measurement is finalized when getting into the evaluation when it’s not. The mechanisms that trigger the problems are completely different, however the penalties are the identical. To deal with these challenges and derive correct sequential assessments for metrics based mostly on a number of observations per unit, it’s necessary to be express in regards to the estimand and the estimator — not all sequential assessments are legitimate in all settings!

In the following a part of this weblog submit sequence, we are going to give recommendation on how one can carry out sequential assessments with longitudinal information, together with sensible concerns and what assessments we’re utilizing at Spotify.  

Acknowledgments

The authors thank Lizzie Eardley and Erik Stenberg for his or her priceless contributions to this submit.

Tags: experimenation